はじめに

次元削減 (dimensionality reduction) とは、データの構造をなるべく保ったまま、特徴量の数を減らすことである。
特徴量の数を減らすことにより、機械学習を高速に実行できたり、データの可視化をしやすくなる利点がある。

次元削減には、射影と多様体学習という2つの主なアプローチがある。射影を使った手法としては、主成分分析 (PCA, Principal Components Analysis) が有名である。一方、本記事で扱うLLEは、多様体学習と呼ばれるアプローチに属する。

多様体

多様体 (manifold) とは、簡単に表すと、局所的に低次元の超平面と見なせる図形のことである。
例えば、以下に示すSwiss Rollは、3次元空間のデータであるが、局所的には2次元の平面と見なせる。
すなわち、データから2次元平面をうまく見つけることができれば、構造を保ったまま3次元から2次元に圧縮できる。

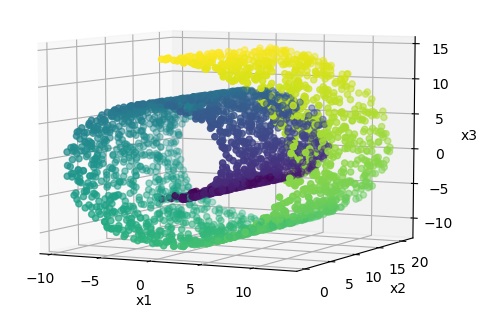
このように、多様体のモデルを見つけることを多様体学習と呼ぶ。多様体学習には以下のように様々な手法がある。

• LLE
• 多次元尺度法 (multi-dimensional scaling, MDS)
• Isomap
• t-SNE (t-distributed Stochastic Neighbor Embedding)
• UMAP (Uniform Manifold Approximation and Projection)

LLEには大域的な位置関係を保存できる長所がある一方、以下の短所もある。

• 多様体が複数ある場合、互いの位置関係をうまく保存できない。
• 圧縮後のデータ位置を再構成する計算量がデータ数の2乗に比例するため、大規模なデータに適用しづらい。

LLEアルゴリズム

LLEのアルゴリズムは、2つのステップでデータ間の局所的な線形モデルを構築し、次元を削減する。

1. 局所的な関係の線形モデル化
2. 関係を維持した次元削減

局所的な関係の線形モデル化

まず、データの各インスタンスに対して、近傍にあるk点のインスタンスを探し、それらインスタンスの線形結合で表すことを考える。ただし、kはハイパーパラメータである。

例として、下図のように2次元空間において5つの点A～Eが与えられた場合に、点Cを近傍インスタンスの線形和として表すことを考える。
k=2とすると、点Cの近傍インスタンスは点B, Dである。
また、点B, C, Dの位置は$\boldsymbol{x^{(B)}, x^{(C)}, x^{(D)}}$で与えられるとする。

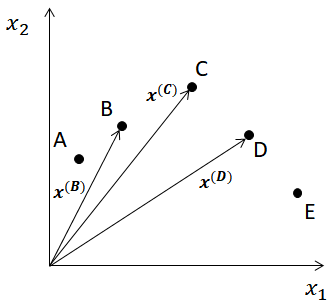
次に、$\boldsymbol{x^{(B)}, x^{(D)}}$の線形結合として次式を考える。
$w_{C, B}\boldsymbol{x^{(B)}} + w_{C, D}\boldsymbol{x^{(D)}}$
ただし、$w_{C, B}, w_{C, D}$は点Cに対する点B, Dの重み係数である。
また、
$w_{C, B}+w_{C, D}=1$
である。

さらに、点Cを点B, Dの線形結合で近似するため、次式が最小となる$w_{C, B}, w_{C, D}$を求める。
$\boldsymbol{x^{(C)}} - (w_{C, B}\boldsymbol{x^{(B)}} + w_{C, D}\boldsymbol{x^{(D)}})$
$\mathrm{subject\ to\ } w_{C, B}+w_{C, D}=1$

下図は、上記の考えを幾何的に示したものである。
図の点B, Dを結ぶ破線は、$\boldsymbol{x^{(B)}, x^{(D)}}$の線形結合を表す。
また、求める係数$w_{C, B}, w_{C, D}$は、
$w_{C, B}\boldsymbol{x^{(B)}} + w_{C, D}\boldsymbol{x^{(D)}}$
と、
$\boldsymbol{x^{(C)}}$
の距離を最小とする値となる。

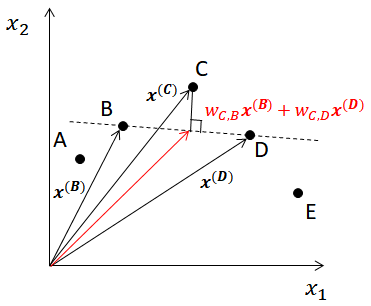
以上、ある点に対する線形モデル化を示したが、全ての点に対して一般化した式を示す。
インスタンスの数を$N$として、重み係数を行列$W\in\mathbb{R}^{N\times N}$にまとめる。
重み係数$w_{i,j}$を$W$の$(i,j)$成分とする。
このとき、線形モデル化とは、次式を最小化する重み行列$W$を求める問題となる。
$$ \sum_{i=1}^{N} \left( \boldsymbol{x^{(i)}} - \sum_{j=1}^{N} w_{i,j} \boldsymbol{x^{(j)}} \right)^2$$

$$ \mathrm{subject\ to\ } \begin{cases} \sum_{j=1}^{N} w_{i,j} = 1 & (\mathrm{for\ } i=1,2,…,N) \\ w_{i,j} = 0 & (\boldsymbol{x^{(j)}} が \boldsymbol{x^{(i)}} の近傍点ではない) \end{cases} $$

関係を維持した次元削減

前節で得られた重み行列$W$を用いて、データの局所的な関係をなるべく維持できるように、圧縮後の次元におけるインスタンスの位置を求める。
圧縮後のインスタンスの位置を$\boldsymbol{y^{(i)} (i=1,2,…,N)}$とする。
ただし、$\boldsymbol{y^{(i)}}$の次元は$\boldsymbol{x^{(i)}}$の次元より小さくなければならない。
このとき、$\boldsymbol{y^{(i)}}$は次式を最小化する値として得られる。
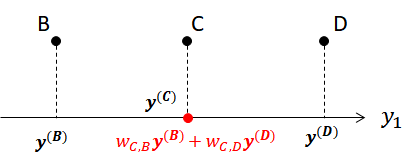
$$ \sum_{i=1}^{N} \left( \boldsymbol{y^{(i)}} - \sum_{j=1}^{N} w_{i,j} \boldsymbol{y^{(j)}} \right)^2 $$

先程の例の続きで説明する。
2次元空間上の点B, C, Dの位置$\boldsymbol{x^{(B)}, x^{(C)}, x^{(D)}}$を1次元空間に圧縮するものとして、圧縮後の位置を$\boldsymbol{y^{(B)}, y^{(C)}, y^{(D)}}$とする。
得られた重み係数$w_{C, B}, w_{C, D}$を用いると、$\boldsymbol{y^{(B)}}$の最適な位置は次式で与えられる（下図参照）。
$$ w_{C, B}\boldsymbol{y^{(B)}} + w_{C, D}\boldsymbol{y^{(D)}} $$

参考

LLEについて、以下のウェブサイトを参考にさせて頂いた。
【多様体学習】LLEとちょっとT-SNE - HELLO CYBERNETICS