はじめに #
ディープラーニングのライブラリの1つであるPyTorchには、自動微分の機能が実装されている。 自動微分を使うと、関数の勾配ベクトルを自動的に求めることができるので、勾配を使った最適化手法を容易に行える。 本記事では、PyTorchのtensorクラスについて簡単に解説し、1階微分、2階微分の求め方ついてまとめる。
※本記事はChainerに関する以下の記事をPyTorch向けに書き直したものである。
PyTorchと最適化 #
PyTorchは、Facebookが提供しているディープラーニング用のライブラリである。 PyTorchには、ニューラルネットワークの学習を高速に行うため、定義した関数の勾配を自動で求める機能が実装されている。 (この機能を使うことで、損失関数を最小化するために、ニューラルネットワークの各ノードの重みをどの方向に更新すれば良いか分かる)
一方、最適化問題を解くとき、最急降下法などの手法では、関数の勾配が必要となる。 関数の勾配を求めるためには、以下の方法がある。
- 関数の導関数を手計算で求める方法
- 数値微分(少しだけ変化させた入力変数を与えて出力の差から勾配を求める)
- 自動微分
問題が複雑な場合、(1)は困難である。 また、(2)は計算時間を要する問題がある。 (3)は、実装に手間が掛かるという欠点があるが、問題ごとに導関数を求める手間も不要で、計算時間も短い利点がある。
PyTorchには(3)の機能がtensorというクラスで実装されているので、最適化に活用するため仕様についてまとめた。 また、最急降下法のPythonでの実装については、過去記事をご参考まで。 直線探索を使った最急降下法をPythonで実装
PyTorchはChainerからフォーク(分岐)しているため、Chainerの特徴を受け継いでいる。
環境 #
| ソフトウェア | バージョン |
|---|---|
| Spyder | 3.3.3 |
| Python | 3.7.3 |
| NumPy | 1.16.2 |
| PyTorch | 1.3.1 |
PyTorchのインストール方法は環境によって異なるため、公式サイトを参考のこと。
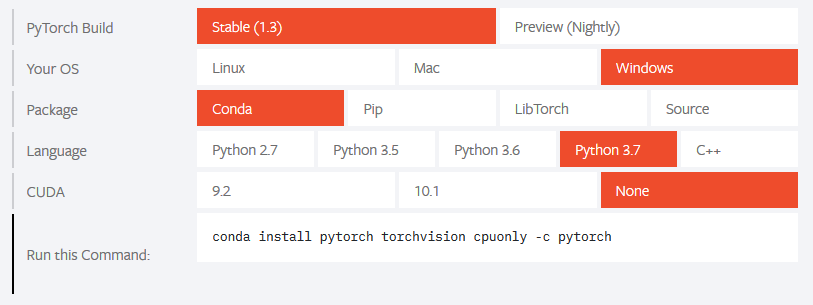
以下の画像のようにPyTorchのバージョンや、OS, インストールパッケージなどを選択し、“Run this Command.“に現れるコマンドを使ってPyTorchをインストールする。
また、以下では、各ライブラリを以下のようにインポートしていることを前提とする。
import numpy as np
import torch
from torch import tensor
tensorクラス #
PyTorchのtensorクラスは、数値の配列データを保持するクラスであり、NumPy配列に近い感覚で扱える。 tensorクラスのオブジェクトを作成するには、tensorクラスの引数に数値、リスト型の配列、またはNumPy配列を与える。
例:
x0 = tensor(1.0)
x1 = tensor([1.0, 2.0])
x2 = tensor(np.array([1.0, 2.0]))
ただし、勾配を求めるためには、requires_gradをTrueにする必要がある(デフォルトではFalse)。
例:
x0 = tensor(1.0, requires_grad=True)
tensorクラスで扱える小数の精度は、16, 32, 64ビットの3種類がある(勾配計算では不要だが、整数やブール型も扱える)。 デフォルトは32ビット小数であり、変更する場合はdtypeオプションに以下の型を指定する。
| 精度 | 型指定 |
|---|---|
| 16ビット | torch.float16 or torch.half |
| 32ビット | torch.float32 or torch.float |
| 64ビット | torch.float64 or torch.double |
例:
x0 = tensor(1.0, dtype=torch.float16)
x1 = tensor([1.0, 2.0], dtype=torch.double)
また、tensorオブジェクト同士の演算ができる(配列のサイズが異なる場合、ブロードキャストされる)。
x0 = tensor(1.0)
x1 = tensor([1.0, 2.0])
print(x0+x1) # tensor([2., 3.])
配列のインデックスを指定して、要素を取り出すことも可能である。
x1 = tensor([1.0, 2.0])
print(x1[1]) # tensor(2.)
tensorオブジェクトのnumpyメソッドを使うと、NumPy配列に変換できる。
x1 = tensor([1.0, 2.0])
x1.numpy() # array([1., 2.], dtype=float32)
さらに、tensorオブジェクトのgrad属性から、勾配のtensor配列を取得できる(詳細は後述)。
1階微分の求め方 #
tensorオブジェクトを使った1階微分の求め方について述べる。 まず、以下の2変数関数を考える。
$$ f(\boldsymbol{x}) = 2x_0^2 + x_1^2 + 2x_0 + x_1, \boldsymbol{x}=[ x_0, x_1 ]^\top $$この関数の勾配ベクトルは次式で与えられる。
$$ \nabla f(\boldsymbol{x}) = \left[ \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1} \right]^\top = [4x_0 + 2, 2x_1 + 1]^\top $$点\( (x_0, x_1)=(1, 2)\)において、関数値と勾配ベクトルはそれぞれ以下のようになる。
$$ f(\boldsymbol{x})=10 \\ \nabla f(\boldsymbol{x}) = [6, 5]^\top $$上記の関数をtensorを使って記述すると以下のようになる。
x = tensor([1.0, 2.0], requires_grad=True)
y = 2*x[0]**2 + x[1]**2 + 2*x[0] + x[1]
関数の値(10)は既に得られている。
>>> y
tensor(10., grad_fn=<AddBackward0>)
grad_fnはyに勾配を計算するための計算グラフが構築されていることを示す属性である。
この段階では勾配はまだ得られておらず、勾配を取得するためにはbackwardメソッドを実行する。
y.backward()
すると、自動微分が実行され、x.gradに勾配が格納される。
>>> x.grad
tensor([6., 5.])
ここで、backwardメソッドを実行する変数がスカラーでなければならないことに注意する。
2つ以上の要素を持つ配列で実行すると、エラーが発生する。
x = tensor([1.0, 2.0], requires_grad=True)
z = 2*x # tensor([2., 4.], grad_fn=<MulBackward0>)
z.backward()
実行結果:
Traceback (most recent call last):
File "<ipython-input-48-40c0c9b0bbab>", line 1, in <module>
z.backward()
File "D:\Anaconda\lib\site-packages\torch\tensor.py", line 166, in backward
torch.autograd.backward(self, gradient, retain_graph, create_graph)
File "D:\Anaconda\lib\site-packages\torch\autograd\__init__.py", line 93, in backward
grad_tensors = _make_grads(tensors, grad_tensors)
File "D:\Anaconda\lib\site-packages\torch\autograd\__init__.py", line 34, in _make_grads
raise RuntimeError("grad can be implicitly created only for scalar outputs")
RuntimeError: grad can be implicitly created only for scalar outputs
エラーメッセージには「スカラーに対してのみ勾配が計算される」とある。
中間変数の勾配を求める場合 #
上記の方法では、以下のようにtensorオブジェクトの演算を2回以上重ねた場合に、中間の変数の勾配が保存されない。
x = tensor(1.0, requires_grad=True)
y = x**2
z = y**2
z.backward()
y.grad # 勾配が格納されない (None)
x.grad # zに対するxの勾配 (tensor(4.))
中間の変数の勾配が欲しい場合には、中間変数のretain_gradメソッドを実行後に、backwardメソッドを実行する。
x = tensor(1.0, requires_grad=True)
y = x**2
z = y**2
y.retain_grad()
z.backward()
y.grad # zに対するyの勾配 (tensor(2.))
x.grad # zに対するxの勾配 (tensor(4.))
2階微分の求め方 #
2階微分を求めるためには以下のようにする。
x = tensor(1.0, requires_grad=True)
y = x**3
grads = torch.autograd.grad(outputs=y, inputs=x, create_graph=True)
grads[0].backward()
x.grad # yに対するxの2階微分 (tensor(6.))
目的変数yを定義後、torch.autograd.grad関数を使って、1階の勾配を取得する。
この関数はoutputsに対するinputsの勾配を計算する関数である。
create_graphをTrueにすることで、微分グラフが構築され、高次の勾配を計算できる。
inputsは複数のtensor配列をとることができるので、戻り値(grads)はタプルである。
そのため、中身を[0]で中身を取り出して、backwardメソッドを実行することで、x.gradに2階微分が格納される。
参考リンク #
- torch.Tensor — PyTorch master documentation
- Automatic differentiation package - torch.autograd — PyTorch master documentation
tensorクラスの作成方法や、簡単な演算について。
自動微分の基本について
3階の勾配や、偏導関数を扱っている
