Scikit-learnのLinearRegressionクラスによる線形回帰

※記事内に商品プロモーションを含むことがあります。

はじめに

線形回帰 (linear regression) は、回帰手法の中で最も単純なものです。例として、以下のグラフのように気温とアイスの売上のデータが与えられているとき、気温からアイスの売上を予測することを考えます。

ice cream sales

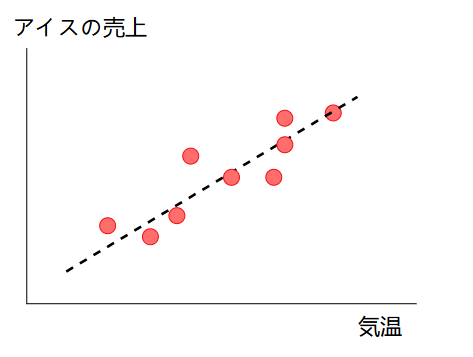
ここで、予測に使用できる変数（気温）を説明変数、予測したい変数（アイスの売上）を目的変数と呼びます（説明変数は独立変数や特徴量、目的変数は従属変数と呼ばれることもあります）。説明変数を$x$、目的変数を$y$と置くと、線形回帰のモデルは次式で表されます。

$$ y = w_1 x + w_0 $$

$w_1$は傾き（係数）、$w_0$は切片です。線形回帰では、説明変数が1増えると目的変数は$w_1$だけ増える、という仮定を置いています。この関係を線形関係と呼びます。また、説明変数が1つだけの線形回帰を単回帰分析と呼びます。

この記事ではPythonとScikit-learnによるサンプルコードも示します。実行環境は以下の通りです。

Python: 3.9.7
NumPy: 1.20.3
sklearn: 0.24.2

重回帰分析

次に、複数の説明変数を考慮したい場合を考えます（アイスの売上には、気温以外に湿度も関係しそうです）。これを重回帰分析 (multiple regression analysis) と呼びます。重回帰のモデルは次式で表されます。

$$ y = w_1 x_1 + w_2 x_2 + … + w_N x_N + w_0 $$

ここで、$w_1, w_2, …, w_N$は重み、$x_1, x_2, …, x_N$は説明変数です。$N$は説明変数の数になります。また、ベクトル表記を使うと重回帰モデルをより簡単に表記できます。重みを$\boldsymbol{w}=[w_1, w_2, .., w_N]^{\top}$, 説明変数を$\boldsymbol{x}=[x_1, x_2, …, x_N]^{\top}$とベクトルにすると、重回帰モデルは次式で表されます。

$$ y = \boldsymbol{w}^{\top} \boldsymbol{x} + w_0 $$

重みと切片$w_0$は、学習データに対して、目的変数と予測値の誤差を最小化するように求められます。この誤差は、全ての学習データに対して、目的変数と予測値の差を二乗して平均した値、すなわち平均二乗誤差 (mean square error, MSE) です。平均二乗誤差は次式で表されます。

$$ \frac{1}{M} \sum_{i=1}^{M} (\boldsymbol{w}^{\top} \boldsymbol{x}^{(i)} + w_0 - y^{(i)})^2 $$

ここで、$M$は学習データの点数です。また、$\boldsymbol{x}^{(i)}$と$y^{(i)}$の$i$は、i番目の学習データであることを示します。平均二乗誤差を最小化する重みと切片は、一般に最小二乗法と呼ばれる手法で求められます。

線形回帰の課題

線形回帰の課題として、データが非線形な場合、モデルを正しく学習できないことがあります。また、重回帰分析を行う場合、過学習に注意する必要があります。

データの非線形性

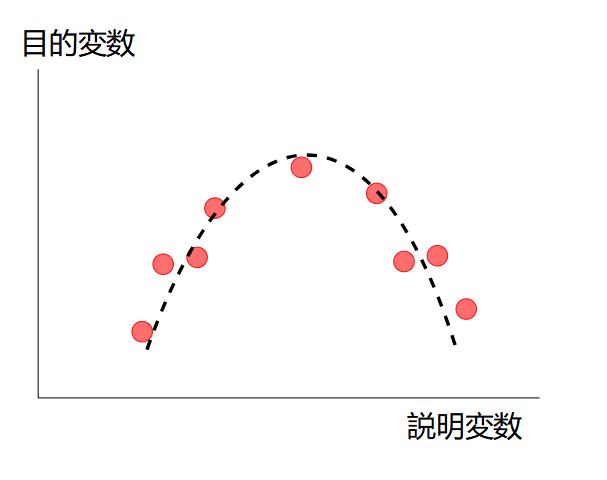
下のようにデータが非線形な場合、線形回帰ではうまくモデルを作れません。SVM回帰や回帰木、ニューラルネットワークなどの非線形な回帰手法を選択する必要があります。

nonlinear data

重回帰分析の過学習

重回帰分析において、相関が強い説明変数があると、推定結果が不安定になります。この問題は多重共線性 (multi-collinearity) と呼ばれます。これを防ぐためにはリッジ回帰、ラッソ回帰、Elastic Netと呼ばれる回帰手法を用います。

scikit-learnの線形回帰

LinearRegressionクラス

scikit-learnではsklearn.linear_model.LinearRegressionというクラスに線形回帰（重回帰を含む）が実装されています。

1
2


sklearn.linear_model.LinearRegression(fit_intercept=True,
    normalize='deprecated', copy_X=True, n_jobs=None, positive=False)

主なパラメータの意味は以下の通りです。

fit_intercept (bool): Trueの場合、切片を計算します。予測モデルが原点を通ることが想定される場合はFalseに設定します。
n_jobs (int): 並列計算数を指定します。-1にすると全てのCPUコアを使用します。

また、主なメソッドは以下の通りです。

fit(X, y): 特徴量X, クラスyを教師データとして学習する。
predict(X): 特徴量Xに対する予測結果を返す。

使用例

LinearRegressionクラスの使用例を示します。X_trainは行がサンプル、列が特徴量の2次元配列です（PandasのDataFrameなどでも可）。y_trainは目的変数の1次元配列です。次に、LinearRegressionクラスのオブジェクトをregという名前で作成します（regはregressorから名付けています）。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


import numpy as np
from sklearn.linear_model import LinearRegression

# 学習データ
X_train = np.array([[0, 1],
                    [3, 2],
                    [5, -2]])
y_train = np.array([3, 10, 23])

reg = LinearRegression()

fitメソッドで学習し、predictメソッドで予測します。予測結果は1次元配列となります。

1
2
3
4
5
6
7
8


# 学習
reg.fit(X_train, y_train)

X_test = np.array([[2, 1],
                   [8, 2]])
# 予測
y_pred = reg.predict(X_test)
print(y_pred)

実行結果

1

[ 8.85714286 24.64285714]

係数を確認するにはreg.coef_, 切片を確認するにはreg.intercept_を表示します。

1
2
3


print(reg.coef_)

print(reg.intercept_)

実行結果

1
2
3


[ 2.92857143 -1.78571429]

4.785714285714291

参考

sklearn.linear_model.LinearRegression — scikit-learn documentation