はじめに #
本記事では、最急降下法と、Armijo条件と呼ばれる直線探索手法について簡単に解説する。
数理工学社の「工学基礎 最適化とその応用」を読んだので、4章「非線形計画法I(無制約最小化問題)」から、直線探索を使った最急降下法をPythonで実装した。
最急降下法とは勾配を用いる最適化手法の1つであり、最急降下法で解の更新幅を求める手法を直線探索という。 本記事では、これらについて簡単に解説し、Pythonで実装したコードを示す。 最後に、実装したコードを使って簡単な2変数関数を最小化する。
また、以降ではライブラリを次のようにインポートしていることを前提とする。
import numpy as np
import matplotlib.pyplot as plt
バージョンは以下の通り。
| ソフトウェア | バージョン |
|---|---|
| python | 3.7.4 |
| numpy | 1.16.4 |
| matplotlib | 3.1.0 |
最急降下法 #
最急降下法 (gradient descent, またはsteepest descent) は、数値最適化手法の1つであり、関数の勾配の方向に解を更新して、最適解に収束させようとするものである。
まず、\(n\)次元ベクトル\(\boldsymbol{x} \in \mathbb{R}^n\)の関数\(f(\boldsymbol{x}) \in \mathbb{R}\)を最小化する問題を考える。 \(f(\boldsymbol{x})\)は微分可能であり、勾配ベクトルは次式で表されるとする。
$$ \nabla f(\boldsymbol{x}) = \left[ \frac{\partial f}{\partial x_1}, ..., \frac{\partial f}{\partial x_n} \right]^\mathrm{T} \in \mathbb{R}^n $$次に、最急降下法のアルゴリズムについて述べる。
- 反復回数を\( k=0\)として、解の初期値\(\boldsymbol{x_k}\)を与える。
- 終了条件を満たせば最適解を\(\boldsymbol{x_k}\)として終了する。そうでなければ、\(\boldsymbol{x_k}\)における勾配\( \nabla f(\boldsymbol{x_k})\)を求める。
- 解の探索方向を\( \boldsymbol{d_k} = -\nabla f(\boldsymbol{x_k})\)とする。
- 探索方向のステップ幅\( \alpha_k\)を直線探索により求め、新たな解を\( \boldsymbol{x_{k+1}} = \boldsymbol{x_k} + \alpha_k \boldsymbol{d_k}\)と更新する。
- \( k \leftarrow k+1\)として、2に戻る。
下図は2変数関数における勾配降下法のイメージである。 等高線は関数の値を示し、\( (x_1, x_2)=(0, 0)\)で最小値をとる。 解候補の点\(\boldsymbol{x_k}\)における探索方向\( \boldsymbol{d_k}\)は、勾配が最も急な方向(等高線と垂直な方向)となる。
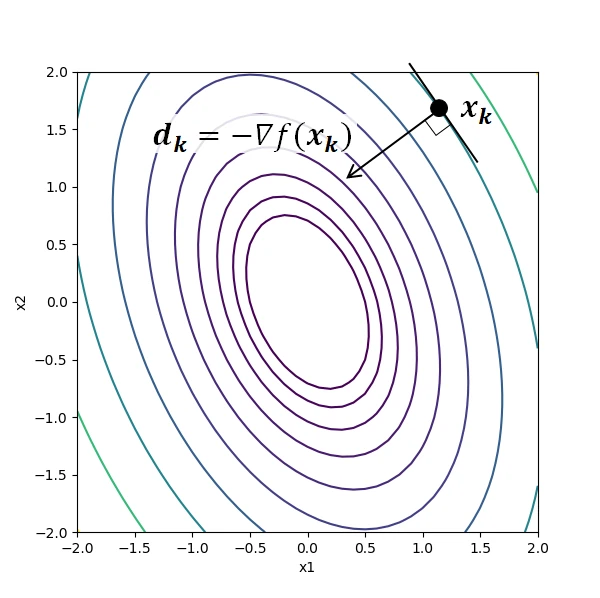
最急降下法には、ステップ幅\( \alpha_k\)が大きすぎると解が発散し、小さすぎると収束が遅くなる問題がある。 この問題に対処できるように\( \alpha_k\)を決める手法が、次節の直線探索である。
直線探索 #
直線探索 (line search) は、最急降下法や準ニュートン法などの最適化手法において得られた解の探索方向に対して、適切な更新幅を求める手法である。 解を大域的に収束させることが求められる。 実用的な直線探索手法としてArmijo(アルミホ)条件とWolf(ウルフ)条件があり、本記事では前者のみ扱う。
Armijo条件とは、\( 0<\xi<1\)である定数\(\xi\)に対して、
$$ f(\boldsymbol{x_k}+\alpha \boldsymbol{d_k}) \leq f(\boldsymbol{x_k}) + \xi \alpha \nabla f(\boldsymbol{x_k})^\mathrm{T} \boldsymbol{d_k} $$を満たす\( \alpha > 0\)を選ぶものである。
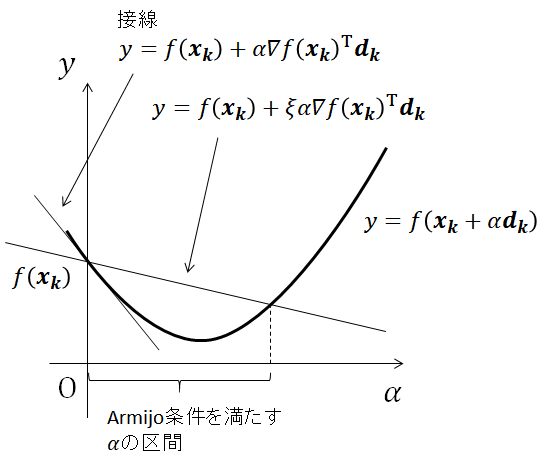
下図にArmijo条件を幾何的に示す。 関数
$$ y=f(\boldsymbol{x_k}+\alpha \boldsymbol{d_k}) $$は\( \boldsymbol{d_k}\)方向の目的関数である。 Armijo条件を満たす\(\alpha\)とは、目的関数
$$ y=f(\boldsymbol{x_k}+\alpha \boldsymbol{d_k}) $$が、直線\( f(\boldsymbol{x_k}) + \xi \alpha \nabla f(\boldsymbol{x_k})^\mathrm{T} \boldsymbol{d_k}\)よりも小さい区間にある。 なお、\( \xi=0\)のとき、直線の値は\( f(\boldsymbol{x_k})\)と等しくなるので解の収束が保障されなくなる。 また、\( \xi=1\)のとき、直線は接線
$$ y=f(\boldsymbol{x_k}) + \alpha \nabla f(\boldsymbol{x_k})^\mathrm{T} \boldsymbol{d_k} $$と一致するので\( \alpha=0\)となり、解の更新幅が0になる。
Armijo条件を満たすステップ幅\( \alpha_k\)を得るアルゴリズムは以下の通り。
- パラメータ\( 0<\xi<1, 0<\tau<1\)を与える。
- 更新幅の初期値を\( \alpha=1\)とおく。
- \( \alpha\)がArmijo条件を満たすならば終了。
- 満たさなければ\( \alpha \leftarrow \tau \alpha\)と更新して3に戻る。
上記のアルゴリズムでは、初めにある程度大きなステップ幅を与え、Armijo条件を満たすまで徐々に小さくしている。そのため、有限回の反復でArmijo条件を満たすステップ幅を得られることが保証される。
Pythonによる実装 #
Armijo条件を用いた最急降下法をPythonで実装した。
funに目的関数、derに勾配を返す関数を与える。また、minimizeメソッドにxを初期値として与えると、最急降下法を実行する。
class GradientDescent:
def __init__(self, fun, der, xi=0.3, tau=0.9, tol=1e-6, ite_max=2000):
self.fun = fun # 目的関数
self.der = der # 関数の勾配
self.xi = xi # Armijo条件の定数
self.tau = tau # 方向微係数の学習率
self.tol = tol # 勾配ベクトルのL2ノルムがこの値より小さくなると計算を停止
self.path = None # 解の点列
self.ite_max = ite_max # 最大反復回数
def minimize(self, x):
path = [x]
for i in range(self.ite_max):
grad = self.der(x)
if np.linalg.norm(grad, ord=2)<self.tol:
break
else:
beta = 1
while self.fun(x - beta*grad) > (self.fun(x) - self.xi*beta*np.dot(grad, grad)):
# Armijo条件を満たすまでループする
beta = self.tau*beta
x = x - beta * grad
path.append(x)
self.opt_x = x # 最適解
self.opt_result = self.fun(x) # 関数の最小値
self.path = np.array(path) # 探索解の推移
最適化の例 #
次式の2変数関数を最小化する例を示す。
$$ f(\boldsymbol{x}) = 2x_1^2 + x_2^2 + x_1 x_2, (\boldsymbol{x}=[ x_1, x_2 ]^\mathrm{T}) $$この関数は、\( (x_1, x_2)=(0, 0)\)で最小値0をとる。 また、勾配ベクトルは次式で与えられる。
$$ \nabla f(\boldsymbol{x}) = \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2} \right]^\mathrm{T} = [4x_1 + x_2, x_1 + 2x_2 ]^\mathrm{T} $$関数値と勾配を求める関数をそれぞれf(x), f_der(x)として定義する。
def f(x):
return 2*x[0]**2 + x[1]**2 + x[0]*x[1]
def f_der(x):
return np.array([4*x[0] + x[1], x[0] + 2*x[1]])
関数の等高線をプロットする。
x1 = np.linspace(-2, 2, 21)
x2 = np.linspace(-2, 2, 21)
x1_mesh, x2_mesh = np.meshgrid(x1, x2)
z = f(np.array((x1_mesh, x2_mesh)))
fig, ax = plt.subplots(figsize=(6, 6))
ax.contour(x1, x2, z, levels=np.logspace(-0.3, 1.2, 10))
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_aspect('equal')
plt.show()
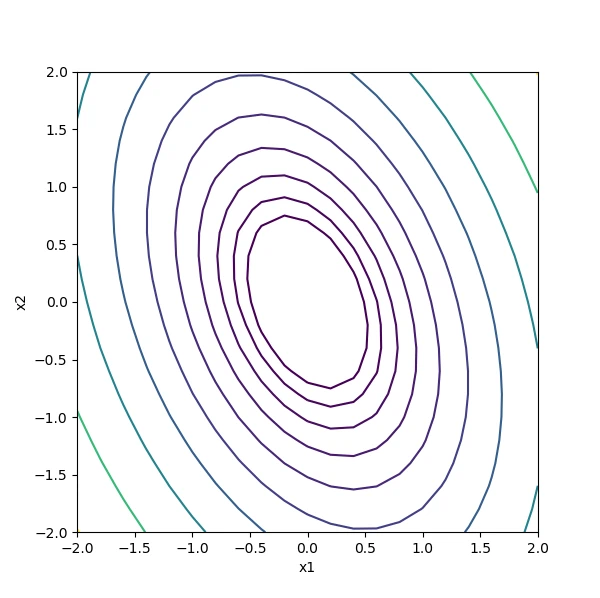
また、勾配をプロットする。
x1 = np.linspace(-2, 2, 21)
x2 = np.linspace(-2, 2, 21)
x1_mesh, x2_mesh = np.meshgrid(x1, x2)
grad = f_der(np.array((x1_mesh, x2_mesh)))
U = grad[0] # x1方向の勾配
V = grad[1] # x2方向の勾配
fig, ax = plt.subplots(figsize=(6, 6))
ax.quiver(x1, x2, U, V, color='blue')
ax.set_aspect('equal')
plt.show()
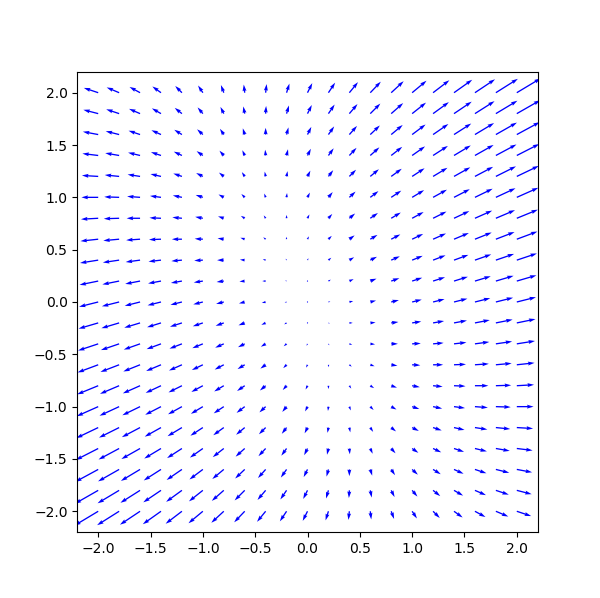
前節のGradientDescentクラスを用いて最急降下法を実行する。
初期値は\( (x_1, x_2)=(1.5, 1.5)\)とする。
gd = GradientDescent(f, f_der)
init = np.array([1.5, 1.5])
gd.minimize(init)
解の推移をプロットする。
path = gd.path
x1 = np.linspace(-2, 2, 21)
x2 = np.linspace(-2, 2, 21)
x1_mesh, x2_mesh = np.meshgrid(x1, x2)
z = f(np.array((x1_mesh, x2_mesh)))
fig, ax = plt.subplots(figsize=(6, 6))
ax.contour(x1, x2, z, levels=np.logspace(-0.3, 1.2, 10))
ax.plot(path[:,0], path[:,1], marker="o")
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_aspect('equal')
plt.show()
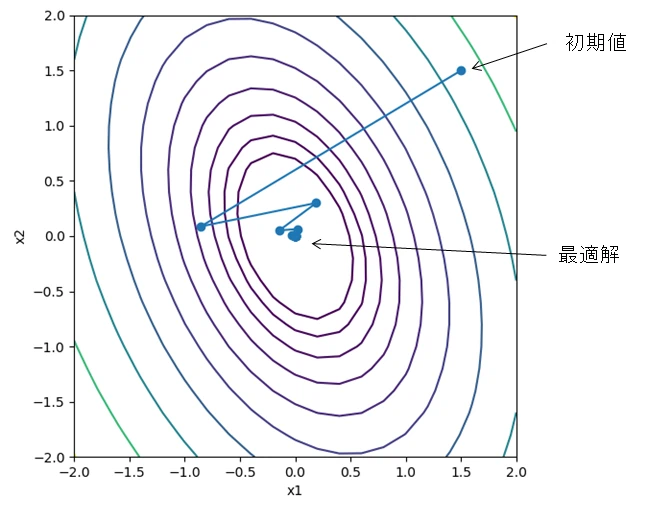
発散せずに最適解へ収束しており、Armijo条件を用いた直線探索がうまく機能していることが分かる。
参考 #
以下のページにステップ幅を固定した最急降下法のコードがあり、実装のベースにさせて頂いた。
直線探索の詳細なアルゴリスムについては以下の書籍を参考とした。
