※記事内に商品プロモーションを含むことがあります。

はじめに

NumPyのfftパッケージを使って、FFT（Fast Fourier Transform, 高速フーリエ変換）による離散信号の周波数解析を行い、信号の振幅を求める。

環境

• NumPy 1.19

FFTの前処理

信号にFFTを掛ける前に、ローパスフィルタと窓関数を掛ける必要がある。詳細は以下のサイトを参照のこと。
11. スペクトル解析と窓関数 (やる夫で学ぶディジタル信号処理)

本記事では簡単のため、これらの前処理を省略する。

FFTを行う離散信号

次の3つの信号を合成して、フーリエ変換を行う離散信号とする。

• 周波数50[Hz], 振幅1.5の正弦波
• 周波数120[Hz], 振幅1の正弦波
• 定数項3

信号のデータ点数は1024, サンプリング周期は0.001[s]とする。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

import numpy as np
import matplotlib.pyplot as plt

N = 1024            # サンプル数
dt = 0.001          # サンプリング周期 [s]
f1, f2 = 50, 120    # 周波数 [Hz]

t = np.arange(0, N*dt, dt) # 時間 [s]
x = 1.5*np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t) + 3 # 信号

fig, ax = plt.subplots()
ax.plot(t, x)
# ax.set_xlim(0, 0.1)
ax.set_xlabel("Time [s]")
ax.set_ylabel("Signal")
ax.grid()
plt.show()

信号の波形を次のグラフに示す。

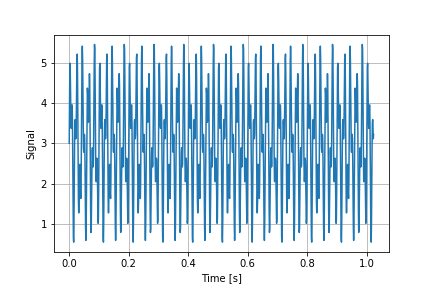
信号を0～0.1[s]の範囲に拡大した図は次の通り。

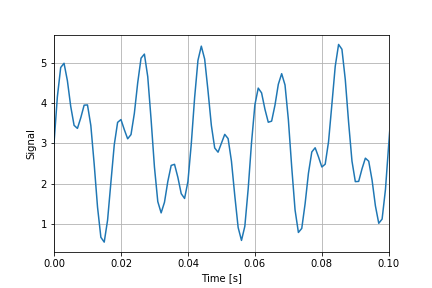
フーリエ変換の関数

前章の信号に対して関数numpy.fft.fft()によりフーリエ変換を行う。

1

numpy.fft.fft(a, n=None, axis=-1, norm=None)

引数の説明は以下の通り。
a: FFTを行う配列。
n: FFTを行うデータ点数。Noneとするとaの長さに等しくなる。
axis: FFTを行う配列の軸方向。指定しなければ、配列の最大次元の方向となる。
norm: "ortho"とすると正規化する。正規化すると変換値が1/√Nになる（Nはデータ点数）。

numpy.fft.fft()の戻り値は、長さnの複素数配列である。

また、関数numpy.fft.fftfreq()によりフーリエ変換の周波数を取得する。

1

numpy.fft.fftfreq(n, d=1.0)

引数の説明は以下の通り。
n: FFTを行うデータ点数。
d: サンプリング周期（デフォルト値は1.0）。

numpy.fft.fftfreq()の戻り値は、周波数を表す配列となる。

FFTの実行とプロット

先程の信号xに対してFFTを行い、変換結果の実部、虚部、周波数をプロットする。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

F = np.fft.fft(x) # 変換結果
freq = np.fft.fftfreq(N, d=dt) # 周波数

fig, ax = plt.subplots(nrows=3, sharex=True, figsize=(6,6))
ax[0].plot(F.real, label="Real part")
ax[0].legend()
ax[1].plot(F.imag, label="Imaginary part")
ax[1].legend()
ax[2].plot(freq, label="Frequency")
ax[2].legend()
ax[2].set_xlabel("Number of data")
plt.show()

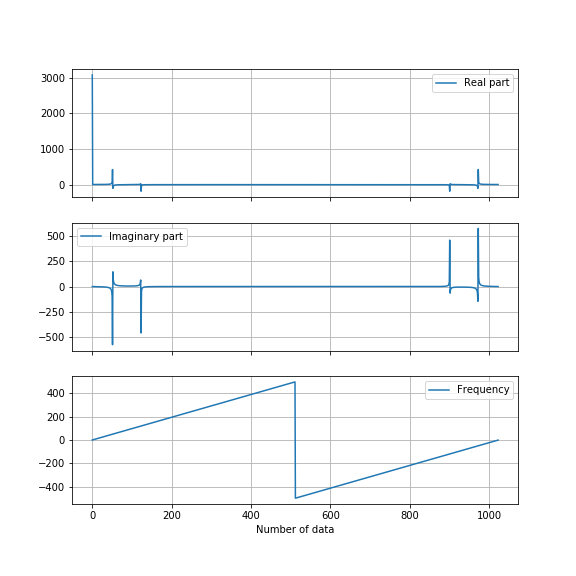
周波数の配列freqにおいて、

• 最初の要素freq[0]は0[Hz]
• 2～N/2 (=512) 番目の要素freq[1:512]は正の周波数
• (N/2+1)番目以降の要素freq[512:]は負の周波数

である。

元の信号の周波数が1000[Hz]であるから、サンプリング定理（または標本化定理）より、その1/2以下の周波数 (500[Hz]以下) でフーリエ変換の結果は有効である。

グラフより、周波数が0, 50, 120, -120, -50[Hz]のときに、実部や虚部がピーク値を持つことが分かる。

最後に元の信号の振幅を求める。FをN/2で割り、絶対値をとると振幅になる。正の周波数領域について振幅をプロットする。

1
2
3
4
5
6
7
8

Amp = np.abs(F/(N/2)) # 振幅

fig, ax = plt.subplots()
ax.plot(freq[1:int(N/2)], Amp[1:int(N/2)])
ax.set_xlabel("Freqency [Hz]")
ax.set_ylabel("Amplitude")
ax.grid()
plt.show()

結果は以下の通り。

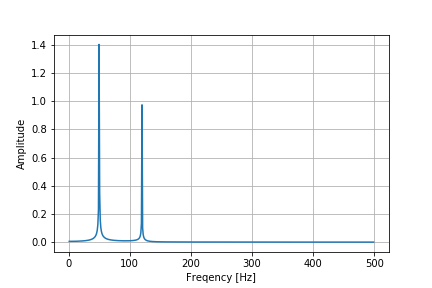
振幅は、周波数50[Hz]で約1.42, 120[Hz]で約0.98となっており、元の値（50[Hz]で約1.5, 120[Hz]で1.0）に近い値となっている。

参考リンク

Discrete Fourier Transform (numpy.fft) — NumPy v1.19 Manual