はじめに #
Pythonの数値解析ライブラリSciPyのinterpolate.interp2dクラスを使って、2次元形状のデータを補間する方法を解説する。補間オプションや、実際の補間例も示す。
また、SciPyには同じく2次元データを補間するinterpolate.griddataもあるが、こちらは関数となっている。
環境 #
- Python 3.8.8
- NumPy 1.20.1
- SciPy 1.6.2
- Matplotlib 3.3.4
Matplotlibはデータの可視化に用いる。
interp2dクラス #
interpolate.interp2dクラスについて解説する。
interp2d(x, y, z, kind='linear', copy=True,
bounds_error=False, fill_value=None)
引数の説明は以下の通り。
x,y: データの座標(1次元配列)z: データ(2次元配列)kind: 補間方法(linear(デフォルト),cubic,quintic)copy: データをコピーする(Falseの場合はデータのアドレスを参照)bounds_error:Trueの場合、補間時の入力座標がx,yの範囲を超えるとエラーを返す。Falseの場合、範囲外ではfill_valueの値を返すfill_value: 外挿領域で返す値。None(デフォルト)の場合、最近傍法で返す
補間により値を求めたい場合は、以下のようにinterp2dインスタンスfに求めたい座標xnew, ynewを渡す。ここで、xnew, ynewはスカラー、1次元配列、2次元配列のいずれも可。
f = interpolate.interp2d(x, y, z, kind='cubic')
znew = f(xnew, ynew)
データの座標x, yは等間隔でなくとも良い。
補間方法 #
interpolate.interp2dクラスのkindオプションで指定可能な補間方法には、以下の3つがある。
linear: 線形補間cubic: 3次補間quintic: 5次補間
linear #
linearでは、双線形 (bilinear) という方法によってデータを補間する(下の画像参照)。
双線形補間では、対象となる座標の近傍4点のデータを用いて、線形近似によって値を求める。画像のように、まずx軸に沿って2点のデータから線形補間を行う。さらに、その結果を用いてy軸に沿って線形補間する。
cubic #
cubicでは、双3次 (bicubic) という方法によってデータを補間する(下の画像参照)。
双3次補間では、対象となる座標の近傍16点のデータを用いて、3次近似によって値を求める。画像のように、まずx軸に沿って4点のデータから3次補間を行う。さらに、その結果を用いてy軸に沿って3次補間する。
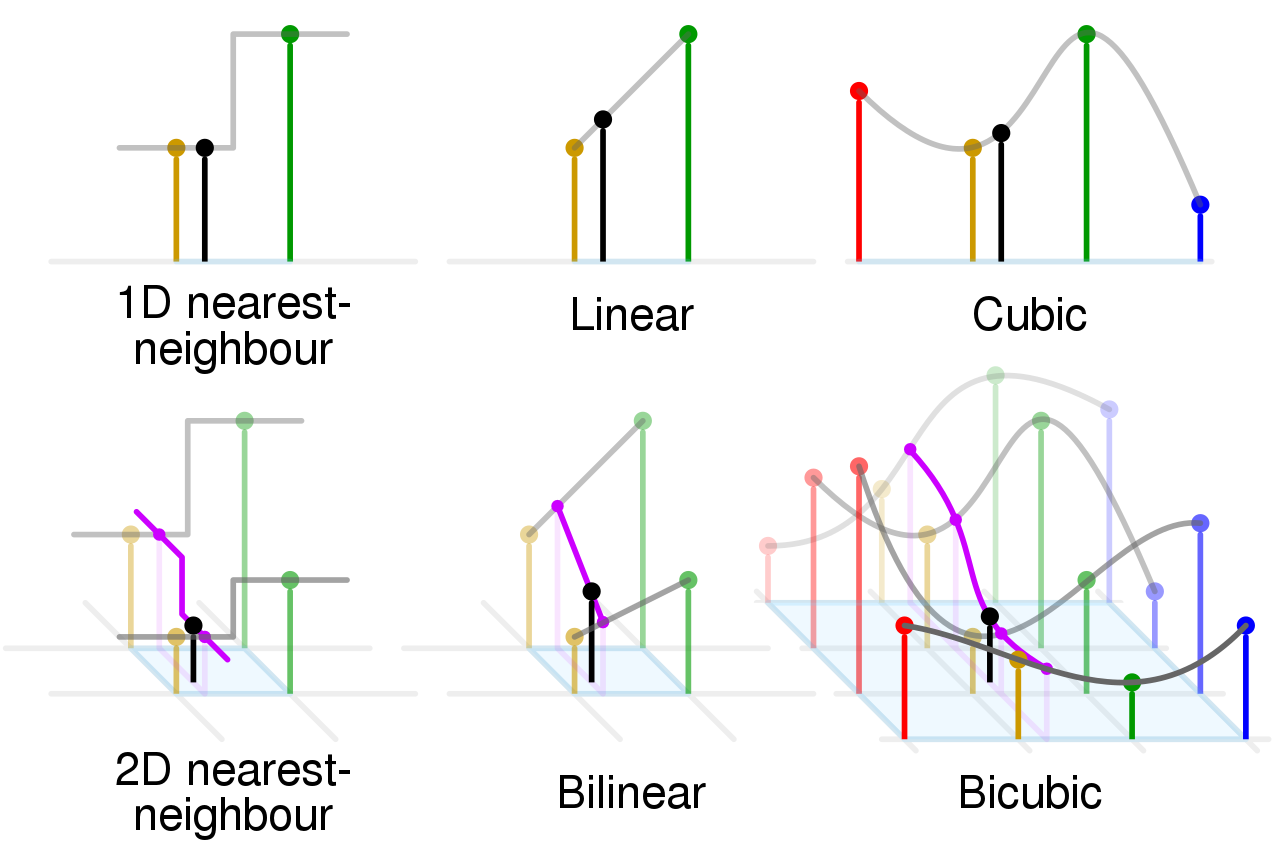
出典:comparison of 1D and 2D interpolation © Cmglee(クリエイティブ・コモンズ・ライセンス)
- math - How to perform bilinear interpolation in Python - Stack Overflow
- 線形補間と双線形補間 ~解説と具体例~ - 理数アラカルト
quintic #
quinticでは上述のような方法で、5次近似によって値を求める。
2次元データの補間例 #
実際に2次元データを補間する。
まず、ライブラリをインポートし、プロット用の関数plot2dを定義する。
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
def plot2d(X, Y, Z, title):
fig, ax = plt.subplots()
mappable = ax.pcolor(X, Y, Z, vmin=-1, vmax=1, shading="nearest")
fig.colorbar(mappable, ax=ax)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title(title)
fig.tight_layout()
plt.show()
ここでは、以下の2変数関数を補間する。
$$ z = \sin (x^2 + y^2) $$参考までに、この関数を\(-6 \le x, y \le 6\)の範囲で、0.1刻みでプロットすると以下のようになる。
x = np.linspace(-3, 3, 61)
y = x.copy()
X, Y = np.meshgrid(x, y)
Z = np.sin(X**2 + Y**2)
plot2d(X, Y, Z, "original")
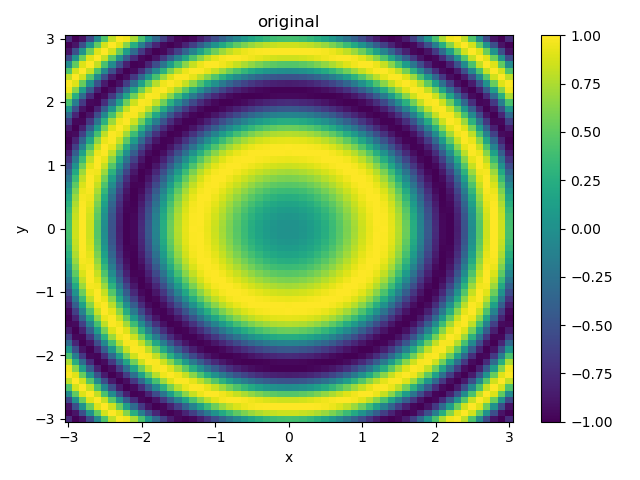
次に、補間に用いるデータとして、同じ範囲で、0.4刻みでプロットすると以下のようになる。
# 荒くしたデータ
x2 = np.linspace(-3, 3, 16)
y2 = x2.copy()
X2, Y2 = np.meshgrid(x2, y2)
Z2 = np.sin(X2**2 + Y2**2)
plot2d(X2, Y2, Z2, "rough")
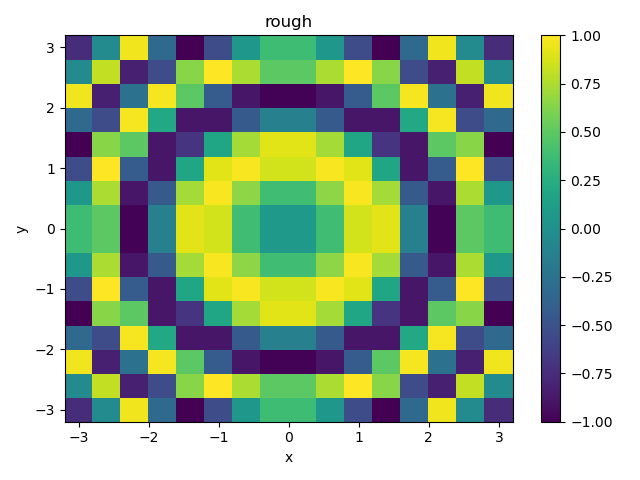
この荒くしたデータを用いて補間した結果を示す。
linear #
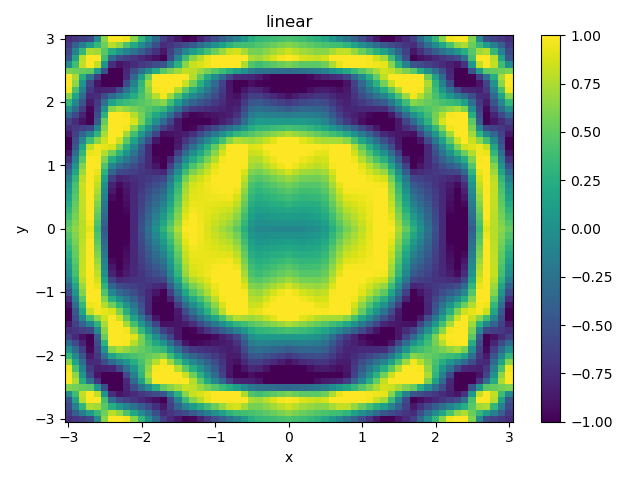
linearで線形補間した結果を示す。データに歪みが生じている。
f_linear = interpolate.interp2d(X2, Y2, Z2, kind='linear')
Z_linear = f_linear(x, y)
plot2d(X, Y, Z_linear, "linear")
cubic #
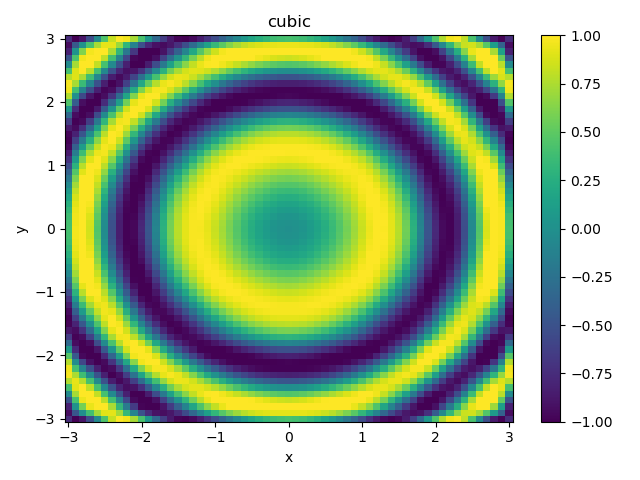
cubicで3次補間した結果を示す。元のデータにかなり近い結果となっている。
f_cubic = interpolate.interp2d(X2, Y2, Z2, kind='cubic')
Z_cubic = f_cubic(x, y)
plot2d(X, Y, Z_cubic, "cubic")
quintic #
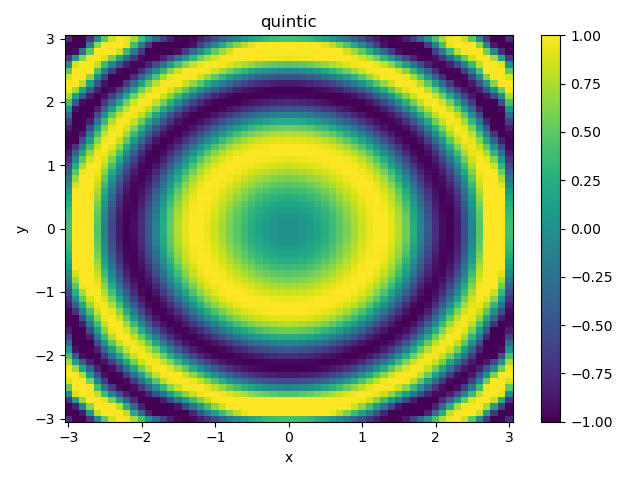
quinticで5次補間した結果を示す。こちらも元のデータにかなり近い結果となっている。
f_quintic = interpolate.interp2d(X2, Y2, Z2, kind='quintic')
Z_quintic = f_quintic(x, y)
plot2d(X, Y, Z_quintic, "quintic")