Scikit-learnのKMeansクラスによるクラスタリング

はじめに

k-means法はよく用いられる単純なクラスタリング手法です。k-means法では、指定した任意の数のグループにデータを分類します。

この記事ではPythonとScikit-learnによるサンプルコードも示します。実行環境は以下の通りです。

Python: 3.9.7
NumPy: 1.20.3
sklearn: 0.24.2
matplotlib: 3.4.3

アルゴリズム

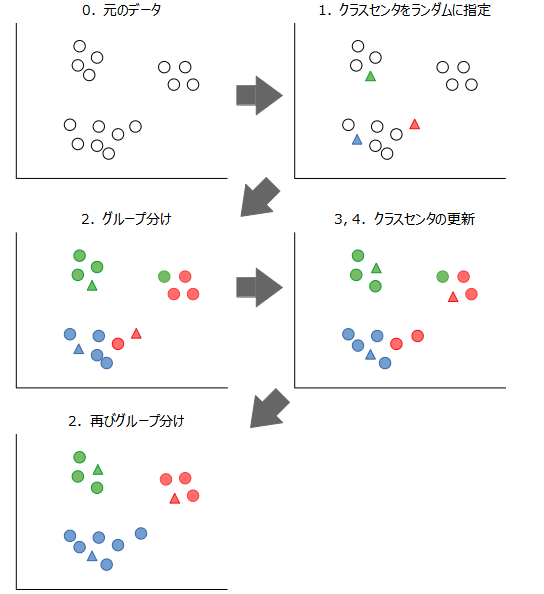
k-means法のアルゴリズムは次の通りです。

ユーザが指定したグループの数（$k$とする）だけ、データをランダムに抽出する。抽出したデータをクラスセンタと呼びます。
全てのデータについて、最も近いクラスセンタにグループ分けする。
各グループについて、属するデータの重心（セントロイド）を計算する。
各グループのセントロイドに最も近い点がクラスセンタであれば、アルゴリズムを停止する。そうでなければ、セントロイドに最も近いデータを新たなクラスセンタとして、2に戻る。

k means algorithm

新たなデータが与えられた場合、そのデータは最も近いクラスセンタのグループに割り当てられます。

特徴

k-means法には以下の長所があります。

アルゴリズムが単純で理解しやすい。
高速に実行できる
大規模なデータにも適用できる。

一方で、以下の短所もあります。

データの分布が非凸な場合にはうまく分類できない。
ユーザがグループの数$k$を指定する必要がある。

scikit-learnのk-means法

KMeansクラス

scikit-learnではsklearn.cluster.KMeansというクラスにk-means法が実装されています。

1
2
3


class sklearn.cluster.KMeans(n_clusters=8, init='k-means++',
    n_init=10, max_iter=300, tol=0.0001, verbose=0,
    random_state=None, copy_x=True, algorithm='lloyd')

主なパラメータの意味は以下の通りです。

n_clusters (int): クラスタの数（デフォルトは8)。
init (str): クラスセンタの初期化方法。デフォルトの'k-means++'はセントロイドが互いに離れるように設定するため、早く収束しやすいです。'random'ではランダムに初期化します。
n_init (int): セントロイドのシードを変えて試行する回数。最も良い結果が返されます（デフォルトは10）。
max_iter (int): 1回の試行あたりの最大反復回数（デフォルトは300）。
random_state (int or None): 乱数シード。常に同じ結果を得たい場合、整数を指定します（デフォルトはNone）。

また、主なメソッドは以下の通りです。

fit(X): 特徴量X（サンプル数×特徴量数の2次元配列）をクラスタリングする。
fit_predict(X): 特徴量Xをクラスタリングし、結果を返す。
predict(X): 特徴量Xに対するクラスの予測結果を返す。

使用例

KMeansクラスの使用例を示します。X_trainは行がサンプル、列が特徴量の2次元配列です（PandasのDataFrameなどでも可）。KMeansクラスのオブジェクトをkmeansという名前で作成し、fit_predictでクラスタリングを行います。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


import numpy as np
from sklearn.cluster import KMeans

# 学習データ
X_train = np.array([[0, 1],
                    [0, 2],
                    [2, 0],
                    [3, 0],
                    [4, 5],
                    [5, 4]])

kmeans = KMeans(n_clusters=3, random_state=0)
cluster_pred = kmeans.fit_predict(X_train)

print(cluster_pred)

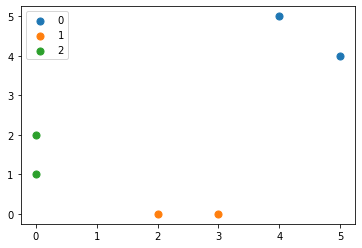
実行結果

クラスタリングの結果は以下になりました。1, 2番目のデータはクラスタ2, 3, 4番目のデータはクラスタ1, …, に属することを示しています。

1

[2 2 1 1 0 0]

最後に、クラスタリングの結果をMatplotlibを使って図示します。

1
2
3
4
5
6
7
8


import matplotlib.pyplot as plt

fig, ax = plt.subplots()
for i in range(3):
    x = X_train[cluster_pred==i]
    ax.scatter(x[:,0], x[:,1], s=50, label=i)
ax.legend()
plt.show()

実行結果

クラスタによって色が異なるようにしています。近くにあるデータ同士が同じクラスタに含まれていることが分かります。

kmeans result

参考

sklearn.cluster.KMeans — scikit-learn documentation