ベイズ推論による多次元ガウス分布の学習

はじめに

「ベイズ推論による機械学習入門」を読んだので、ベイズ推論（ベイズ推定）への理解を深めるため、多次元ガウス分布の学習をPythonで実装した。
参考にしたのは、講談社機械学習スタートアップシリーズの「ベイズ推論による機械学習入門」（須山敦志著）。3.4節「多次元ガウス分布の学習と予測」から、平均と精度（分散共分散行列）が共に未知の場合における学習について実装した。
また、学習したパラメータを用いて、未観測データを予測するための分布（予測分布）も構築した。

なお、以下のブログに離散確率分布（ベルヌーイ分布・カテゴリ分布・ポアソン分布）と1次元ガウス分布の学習の実装例があったため、併せて参考にさせて頂いた。
「ベイズ推論による機械学習入門」を読んだので実験してみた (その1)

環境

ソフトウェア	バージョン
python	3.6.5
numpy	1.14.3
scipy	1.1.0
matplotlib	2.2.2

以下では、各ライブラリを以下のようにインポートしていることを前提とする。

1
2
3
4


import math
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt

ベイズ学習について

ベイズ学習は、観測データと未知パラメータに対する同時確率分布を構築し、観測データが得られたときの未知パラメータの事後分布を求める手法である。
ここでは、多次元ガウス分布の平均と精度が未知パラメータとなる。

多次元ガウス分布のベイズ推論

$D$次元の多次元ガウス分布は、次式で表される。

$$ \mathcal{N}(x|\mu, \Sigma) = \frac{1}{\sqrt{(2\pi)^D|\Sigma|}} \exp \biggl( -\frac{1}{2} (x-\mu)^\top \Sigma^{-1} (x-\mu) \biggl) $$

ここで、$ \mu \in \mathbb{R}^D$ は平均、$ \Sigma \in \mathbb{R}^{D \times D}$は分散共分散行列である。
ただし、$\Sigma$は正定値行列（固有値が全て非負）でなければならない。
後々の数式を簡単にするため、精度行列$\Lambda = \Sigma^{-1}$を導入する。
$\mu, \Lambda$が推定したいパラメータになる。

$\mu, \Lambda$の確率分布を表現する共役事前分布は、ガウス・ウィシャート分布となる。

$$ \begin{array}{rl} p(\mu, \Lambda) &=& NW(\mu, \Lambda | m, \beta, \nu, W) \\ &=& \mathcal{N}(\mu | m, (\beta \Lambda)^{-1}) \mathcal{W}(\Lambda | \nu, W) \end{array} $$

ここで、$m, \beta, \nu, W$はガウス・ウィシャート分布のパラメータである。初期値は以下の条件を満たすように適当に与える。

$m \in \mathcal{R}^{D}$: 実数ベクトル
$\beta \in \mathcal{R}$: 実数
$\nu \in \mathcal{R}$: $\nu > D-1$を満たす実数
$W \in \mathcal{R}^{D \times D}$: 正定値行列（固有値が全て非負）

事後分布を計算すると、ガウス・ウィシャート分布のパラメータはそれぞれ以下のように与えられる（詳細は本を参照）。

$$ \hat{\beta} = N + \beta $$
$$ \hat{m} = \frac{1}{\hat{\beta}} \left( \sum_{n=1}^N x_n + \beta m \right) $$
$$ \hat{W}^{-1} = \sum_{n=1}^N x_n x_n^{\top} + \beta mm^{\top} - \hat{\beta} \hat{m} \hat{m}^{\top} + W^{-1} $$
$$ \hat{\nu} = N + \nu $$

学習したガウス・ウィシャート分布のパラメータを使って、未観測のデータ$x$を予測する。予測分布は$x\in \mathbb{R}^D$上の多次元版のスチューデントのt分布となる。

$$ \mathrm{St} (x|\mu_s, \Lambda_s, \nu_s) = \frac{\Gamma( \frac{\nu_s+D}{2}) }{\Gamma( \frac{\nu_s}{2})} \frac{|\Lambda_s|^{\frac{1}{2}}}{(\pi \nu_s)^{\frac{D}{2}}} \biggl( 1+\frac{1}{\nu_s} (x-\mu_s)^{\top} \Lambda_s (x-\mu_s) \biggl)^{-\frac{\nu_s +D}{2} } $$

ここで、スチューデントのt分布のパラメータは、ガウス・ウィシャート分布のパラメータを使って次式で与えられる。

$$ \mu_s = m $$
$$ \Lambda_s = \frac{(1-D+\nu)\beta}{1+\beta}W $$
$$ \nu_s = 1-D+\nu $$

また、$\Gamma(\bullet)$はガンマ関数と呼ばれる関数である。

学習が進むにつれて、スチューデントのt分布の形状は、元の多次元ガウス分布の形状に近づいていく。

実装

ガウス・ウィシャート分布のパラメータ推定

観測データXから、ガウス・ウィシャート分布のパラメータの推定値$\hat{m}, \hat{\beta}, \hat{\nu}, \hat{W}$を推定する関数を以下のように実装する。
ただし、計算効率は重視せず、数式通りに実装することを優先している。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


def multivariate_normal_fit(X):
    N = X.shape[0] # Number of samples
    D = X.shape[1] # Dimension of sample
    
    beta  = 1
    m     = np.zeros(D)
    W_inv = np.linalg.inv(np.diag(np.ones(D)))
    nu    = D
    
    beta_hat = N + beta
    m_hat    = (X.sum(axis=0)+beta*m)/beta_hat
    
    X_sum = np.zeros([D, D])
    for i in range(N):
        X_sum += np.dot(X[i].reshape(-1,1), X[i].reshape(1,-1))
    
    W_hat_inv = X_sum + beta*np.dot(m.reshape(-1,1), m.reshape(1,-1)) \
            - beta_hat*np.dot(m_hat.reshape(-1,1), m_hat.reshape(1,-1)) + W_inv
    nu_hat = N + nu
    
    return m_hat, beta_hat, nu_hat, W_hat_inv

多次元版のスチューデントのt分布

学習後の確率分布を確認するため、多次元版のスチューデントのt分布をクラスとして実装する。
確率密度関数 (Probability Density Function, PDF) を求めるため、pdfメソッドを用意した。pdfメソッドに配列を引数として与えると、その配列に対応する確率を返す。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class multivariate_student_t():
    def __init__(self, mu, lam, nu):
        # mu: D size array, lam: DxD matrix, nu: scalar
        self.D   = mu.shape[0]
        self.mu  = mu
        self.lam = lam
        self.nu  = nu
        
    def pdf(self, x):
        temp1 = np.exp( math.lgamma((self.nu+self.D)/2) - math.lgamma(self.nu/2) )
        temp2 = np.sqrt(np.linalg.det(self.lam)) / (np.pi*self.nu)**(self.D/2) 
        
        if x.shape[0]==1:
            temp3 = 1 + np.dot(np.dot((x-self.mu).T, self.lam),  x-self.mu)/self.nu
        else:
            temp3 = []
            for a in x:
                temp3 += [1 + np.dot(np.dot((a-self.mu).T, self.lam),  a-self.mu)/self.nu]
        
        temp4 = -(self.nu+self.D)/2
        return temp1*temp2*(np.array(temp3)**temp4)

ここで、ガンマ関数の自然対数を返すmath.lgammaで実装した。
ガンマ関数math.gammaは大きな値を取り得ることがあり、以下のようにオーバーフローが生じる場合があるためである。

1
2
3
4
5
6
7


>>> math.gamma(200)
Traceback (most recent call last):

  File "<ipython-input-31-4fa9aaaad750>", line 1, in <module>
    math.gamma(200)

OverflowError: math range error

パラメータの学習

学習の結果を確認する。図示できるように、データの次元は$D=2$とする。
まず、多次元ガウス分布に従うサンプルデータを生成する。
ここで、データの平均は$(x_1, x_2)=(0, 1)$であり、正の相関を持つ。

1
2
3
4
5
6
7
8


np.random.seed(0)

mean = np.array([0, 1])
cov  = np.array([[2, 1],
                 [1, 2]])
Ns   = 100                # Number of samples

X = np.random.multivariate_normal(mean, cov, Ns) # Sample data

サンプルデータを散布図にプロットする。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


fig, ax = plt.subplots(figsize=(8, 4))
ax.scatter(X[:,0], X[:,1])
ax.axis('square')
ax.set_xlim(-5,5)
ax.set_ylim(-5,5)
ax.grid()
ax.set_xlabel("x1")
ax.set_ylabel("x2")
fig.tight_layout()
plt.show()

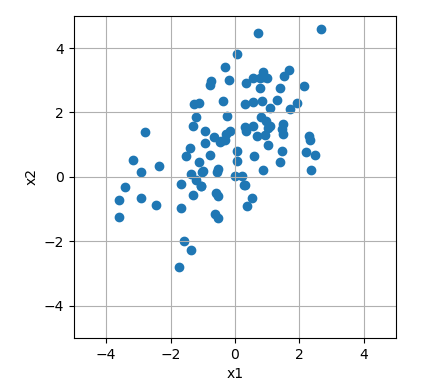
$scatter_2d_normal_dist$

次に、関数multivariate_normal_fitから、ガウス・ウィシャート分布のパラメータを求める。

1

m_hat, beta_hat, nu_hat, W_hat_inv = multivariate_normal_fit(X)

得られたパラメータをスチューデントのt分布のパラメータに変換し、
multivariate_student_tオブジェクトを作成する。

1
2
3
4
5
6


D       = m_hat.shape[0]
mu_hat  = m_hat
lam_hat = (1-D+nu_hat)*beta_hat*np.linalg.inv(W_hat_inv) / (1+beta_hat) 
nu_hat  = 1 - D + nu_hat

mt = multivariate_student_t(mu_hat, lam_hat, nu_hat)

最後に、元のガウス分布の形状と、推定したスチューデントのt分布の形状を比較する。
両確率分布の確率を、x1, x2とも-5～5の範囲で求める。

1
2
3
4
5
6
7
8


X1, X2 = np.meshgrid(np.arange(-5, 5, 0.1), np.arange(-5, 5, 0.1))
Y = np.vstack([X1.ravel(), X2.ravel()]).T

mn_pdf = scipy.stats.multivariate_normal.pdf(Y, mean=mean, cov=cov)
mn_pdf = mn_pdf.reshape(X1.shape[0], -1)

mt_pdf = mt.pdf(Y)
mt_pdf = mt_pdf.reshape(X1.shape[0], -1)

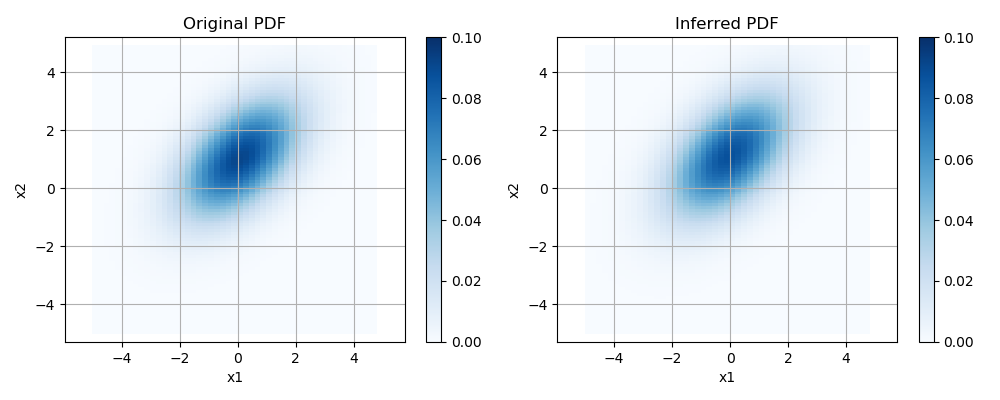
これらをヒートマップに表示する。色が濃いほど確率が高いことを表す。
このように、推定した確率密度関数と、元の確率密度関数はほぼ一致している。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


fig, ax = plt.subplots(ncols=2, figsize=(10, 4))
ax0 = ax[0].pcolor(X1, X2, mn_pdf, cmap="Blues", vmin=0, vmax=0.1)
ax1 = ax[1].pcolor(X1, X2, mt_pdf, cmap="Blues", vmin=0, vmax=0.1)
for i in range(2):
    ax[i].axis('equal')
    ax[i].grid()
    ax[i].set_xlabel("x1")
    ax[i].set_ylabel("x2")
ax[0].set_title("Original PDF")
ax[1].set_title("Inferred PDF")
plt.colorbar(ax=ax[0], mappable=ax0)
plt.colorbar(ax=ax[1], mappable=ax1)
fig.tight_layout()
plt.show()

$pdf_heatmap$

以上をまとめたコードは以下の通り。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102


import math
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt

class multivariate_student_t():
    def __init__(self, mu, lam, nu):
        # mu: D size array, lam: DxD matrix, nu: scalar
        self.D   = mu.shape[0]
        self.mu  = mu
        self.lam = lam
        self.nu  = nu
        
    def pdf(self, x):
        temp1 = np.exp( math.lgamma((self.nu+self.D)/2) - math.lgamma(self.nu/2) )
        temp2 = np.sqrt(np.linalg.det(self.lam)) / (np.pi*self.nu)**(self.D/2) 
        
        if x.shape[0]==1:
            temp3 = 1 + np.dot(np.dot((x-self.mu).T, self.lam),  x-self.mu)/self.nu
        else:
            temp3 = []
            for a in x:
                temp3 += [1 + np.dot(np.dot((a-self.mu).T, self.lam),  a-self.mu)/self.nu]
        
        temp4 = -(self.nu+self.D)/2
        return temp1*temp2*(np.array(temp3)**temp4)

def multivariate_normal_fit(X):
    N = X.shape[0] # Number of samples
    D = X.shape[1] # Dimension of sample
    
    beta  = 1
    m     = np.zeros(D)
    W_inv = np.linalg.inv(np.diag(np.ones(D)))
    nu    = D
    
    beta_hat = N + beta
    m_hat    = (X.sum(axis=0)+beta*m)/beta_hat
    
    X_sum = np.zeros([D, D])
    for i in range(N):
        X_sum += np.dot(X[i].reshape(-1,1), X[i].reshape(1,-1))
    
    W_hat_inv = X_sum + beta*np.dot(m.reshape(-1,1), m.reshape(1,-1)) \
            - beta_hat*np.dot(m_hat.reshape(-1,1), m_hat.reshape(1,-1)) + W_inv
    nu_hat = N + nu
    
    return m_hat, beta_hat, nu_hat, W_hat_inv

if __name__=="__main__":
    np.random.seed(0)
    
    mean = np.array([0, 1])
    cov  = np.array([[2, 1],
                     [1, 2]])
    Ns   = 100                # Number of samples
    
    X = np.random.multivariate_normal(mean, cov, Ns) # Sample data
    
    fig, ax = plt.subplots(figsize=(8, 4))
    ax.scatter(X[:,0], X[:,1])
    ax.axis('square')
    ax.set_xlim(-5,5)
    ax.set_ylim(-5,5)
    ax.grid()
    ax.set_xlabel("x1")
    ax.set_ylabel("x2")
    fig.tight_layout()
    plt.show()
    
    m_hat, beta_hat, nu_hat, W_hat_inv = multivariate_normal_fit(X)
    
    D       = m_hat.shape[0]
    mu_hat  = m_hat
    lam_hat = (1-D+nu_hat)*beta_hat*np.linalg.inv(W_hat_inv) / (1+beta_hat) 
    nu_hat  = 1 - D + nu_hat
    
    mt = multivariate_student_t(mu_hat, lam_hat, nu_hat)
    
    X1, X2 = np.meshgrid(np.arange(-5, 5, 0.1), np.arange(-5, 5, 0.1))
    Y = np.vstack([X1.ravel(), X2.ravel()]).T
    
    mn_pdf = scipy.stats.multivariate_normal.pdf(Y, mean=mean, cov=cov)
    mn_pdf = mn_pdf.reshape(X1.shape[0], -1)
    
    mt_pdf = mt.pdf(Y)
    mt_pdf = mt_pdf.reshape(X1.shape[0], -1)
    
    fig, ax = plt.subplots(ncols=2, figsize=(10, 4))
    ax0 = ax[0].pcolor(X1, X2, mn_pdf, cmap="Blues", vmin=0, vmax=0.1)
    ax1 = ax[1].pcolor(X1, X2, mt_pdf, cmap="Blues", vmin=0, vmax=0.1)
    for i in range(2):
        ax[i].axis('equal')
        ax[i].grid()
        ax[i].set_xlabel("x1")
        ax[i].set_ylabel("x2")
    ax[0].set_title("Original PDF")
    ax[1].set_title("Inferred PDF")
    plt.colorbar(ax=ax[0], mappable=ax0)
    plt.colorbar(ax=ax[1], mappable=ax1)
    fig.tight_layout()
    plt.show()

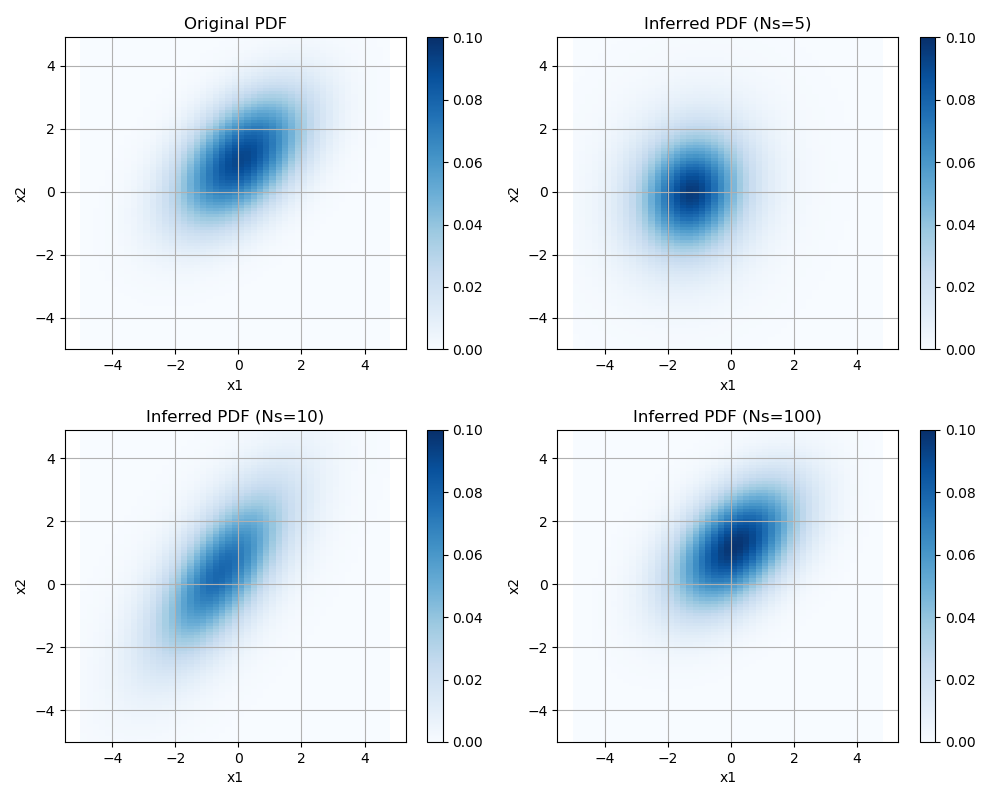
また、学習データのサンプル数Nsを5, 10, 100と変えて、推定精度に与える影響を調べる。下図のように、Nsが増えるほど、元の確率密度分布（左上）に近づいている。

$pdf_heatmap_2$