はじめに #
最適制御問題を解く手法の1つである、Direct Single Shooting法のアルゴリズムをまとめた。
最適制御問題を解く手法の分類を以下の図に示す(Dynamic optimization with CasADiより)。
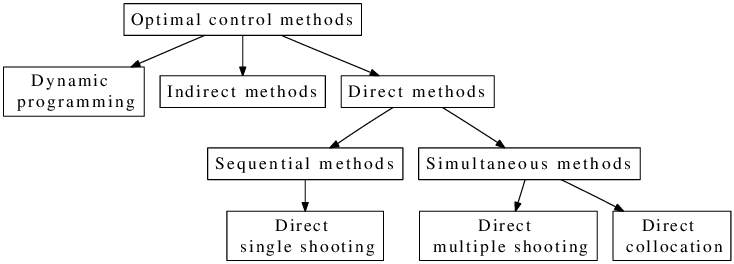
Direct Single Shooting法は、直接法 (direct method) と狙い撃ち法 (shooting method) を組み合わせた手法である。
直接法の特徴は以下の通り。
- 時刻方向に離散化して最適化する
- 解の精度はあまり高くない
- 定式化が容易
狙い撃ち方の特徴は以下の通り。
- シミュレーションベース(システムの動特性を微分方程式で扱える)
- システムや制約が複雑な問題には向かない
Direct Single Shooting法が向いているのは、飛行機やロケットなどの経路最適化問題である。反対に、化学プラントのような変数や制約が多く、非線形性が強いシステムには向いていない。
また、Direct Single Shooting法を拡張した手法としてDirect Multiple Shooting法がある。Direct Multiple Shooting法では、離散化された各時刻で並列にシミュレーションを実行する。「ある時間幅の終端におけるシステムの状態と、次の時間幅の始端におけるシステムの状態が等しい」という制約を導入することで、次の時間幅との連続性を担保する。 同じ最適制御問題をDirect Single Shooting法とDirect Multiple Shooting法で解いた場合、後者では変数が増加する代わりに、スパースな最適化問題となる。
本記事では最初に、最適制御について定式化を兼ねて解説する。最後にDirect Single Shooting法のアルゴリズムを示す。
最適制御 #
最適制御とは、動的なシステムに対して性能を向上させるような評価関数を設定し、その評価関数を最小化するように、システムの入力を決定する制御方法である。 たとえば旅客機の場合、燃料の消費量を評価関数として、これが最小となるように操舵角やエンジン出力を求める最適制御問題が考えられる。 なお、動的なシステムとは、ある時刻のシステムの状態が、以前の時刻の状態に依存するシステムのことである(一方、静的なシステムでは、ある時刻における入力のみでその時刻の状態が決まる)。
次に、最適制御問題を一般的な形で定式化する。まず、時刻を\(t\)とおき、システムの状態を\(x(t)\), 入力を\(u(t)\)として、システムの動特性が\(\dot{x}(t)=f(x(t), u(t))\)で記述されると定義する。 このとき、最適制御問題は以下の最小化問題となる。
$$ \min_{x(t), u(t)} \int_{t_0}^{t_f} l(x(t), u(t)) \mathrm{d}t + m(x(t_f)) \\\ \begin{array}{ll} \mathrm{subject \ to} & \dot{x}(t)=f(x(t), u(t)) \\\ & g(x(t), u(t)) = 0 \\\ & h(x(t), u(t)) > 0 \end{array} $$変数の意味は以下の通り。
- \(t_0\), \(t_f\): 制御の開始時刻、終了時刻
- \(l(x, u)\): \(t_0\)~\(t_f\)における評価関数
- \(m(x)\): 終了時刻における状態\(x\)に対する評価関数
- \(g(x, u), h(x, u)\): システムの等式制約、不等式制約
すなわち、最適制御問題は、システムの動特性およびその他の制約を満たしながら、与えられた評価関数を最小化することになる。 前述の旅客機の例では、\(g(x, u), h(x, u)\)は入力(操舵角やエンジン出力)の上限や、飛行機の角度(背面飛行をしない等)の制限になる。また、\(l(x, u), m(x)\)は現在位置と目的地までとの距離の誤差に対するペナルティなどになるだろう。
Direct Single Shooting法 #
Direct Single Shooting法では、初期状態\(x(t_0)\)(の一部)と各時刻の入力\(u(t)\)を求める。
Direct Single Shooting法の基本的な概念は以下の通り。
- 制御の開始から終了まで、時刻を\(t_0, t_1, ..., t_f\)と(等間隔に)分割する
- 分割された時刻ごとに、その時間幅内で入力\(u(t)\)の値は一定とする
- 時間幅ごとに状態\(x(t)\)を数値積分により求める
以下のグラフのイメージになる(Moritz Diehlより)。 点線が入力\(u\)、実線が状態\(x\)となる。
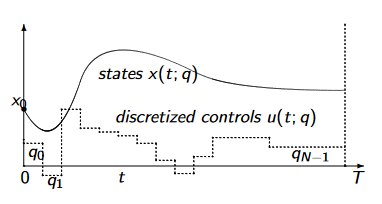
Direct Single Shooting法のアルゴリズムは以下の通り。
- 解の初期値\(x(t_0), u(t_0), u(t_1), ..., u(t_f)\)を設定
- 評価関数\(J=0\)を準備
- 等式制約・不等式制約の配列\(g=[], h=[]\)を準備
- for \(k = 0\) to \(N\) do
- \(\qquad x_{k+1} = \int f(x_k, u_k)\)
- \(\qquad J += \int l(x_k, u_k)\)
- \(\qquad h\).append([\(x_k - \underline{x}\), \(\overline{x} - x_k\)])
- \(\qquad h\).append([\(u_k - \underline{u}\), \(\overline{u} - u_k\)])
- \(\qquad\)その他、制約があれば\(g, h\)に追加
- end for
- \(J += m(x_{N+1})\)
- 制約\(g, h\)の下で\(J\)を最小化する非線形最適化問題を解く
