※記事内に商品プロモーションを含むことがあります。
はじめに
CasADiは自動微分と非線形最適化のためのライブラリである。C++で実装されており、C++, Python, Matlab, Octaveのインターフェースを備えている。
本記事ではPythonを使い、CasADiで常微分方程式を解く方法をまとめた。
例として示す問題は以下の2つである。
環境は以下の通り。
| ソフトウェア |
バージョン |
| Python |
3.8.5 |
| NumPy |
1.19.2 |
| CasADi |
3.5.5 |
| Matplotlib |
3.3.2 |
CasADiはpipでインストールできる。
pip install casadi
また、本記事では以下の通りライブラリをインポートしていることを前提とする。
1
2
3
|
import numpy as np
import casadi as ca
import matplotlib.pyplot as plt
|
リンク
1階常微分方程式
対象とする問題
次式の1階の常微分方程式を考える。
$$ x' = -x + 2 $$
ただし、独立変数を時間$t$とし、未知関数$x(t)$とする。この方程式の一般解は以下となる（$c$は定数）。
$$ x(t) = 2 + ce^{-t} $$
また、初期条件を$x(0)=0$とおくと$c=-2$であるから、初期値問題の解は以下となる。
$$ x(t) = 2 - 2 e^{-t} $$
この問題をCasADiで解く。簡単のため、以下の2段階に分けて説明する。
- ある最終時刻における解を求める
- ある時間範囲の解の推移を求める
最終時刻の解を得る
時間の範囲を0～10[s]とし、初期値$x(0)=0$を与えたときの、$t=10$における解を求める。
コードは以下のようになる。
1
2
3
4
5
6
7
8
9
10
|
x = ca.MX.sym("x") # 未知関数
rhs = -x + 2 # 微分方程式の右辺
ode = {'x': x,
'ode': rhs}
opts = {'t0':0, # 初期時刻
'tf':10} # 最終時刻
F = ca.integrator('F', 'cvodes', ode, opts)
res = F(x0=[0]) # 初期値を指定して解く
print(res['xf']) # 最終時刻の解
|
実行結果
コードについて簡単に解説する。
rhsは微分方程式の右辺(right hand side)の略である。
ca.integratorには以下を順に指定する。
- 方程式の名前
- 微分方程式のソルバ
- 微分方程式
- オプション（初期時刻、最終時刻）
時刻推移をプロットする
解の時刻推移を得るには、取得したい時刻ごとに微分方程式を解き、最終時刻の解を次の時刻の初期値とする。
例えば、0～10[s]の範囲で0.1[s]周期で解を得たい場合、以下のようにfor文で実行する。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
dt = 0.1 # サンプル周期
times = np.arange(0, 10+dt, dt)
x_history = [0] # xの時刻歴データ
x = ca.MX.sym("x") # 未知関数
rhs = -x + 2 # 微分方程式の右辺
ode = {'x': x,
'ode': rhs}
opts = {'t0':0,
'tf':dt}
F = ca.integrator('F', 'cvodes', ode, opts)
for t in times[:-1]:
res = F(x0=x_history[-1])
x_history += res['xf'].toarray().tolist()[0]
fig, ax = plt.subplots()
ax.plot(times, x_history)
ax.set_xlabel('t')
ax.set_ylabel('x')
ax.grid()
plt.show()
|
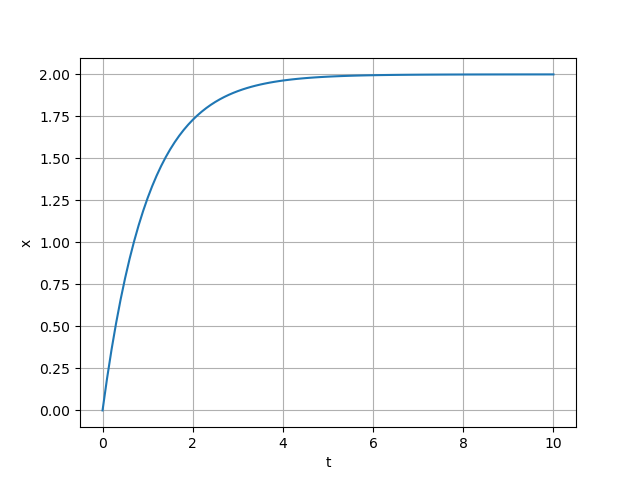
実行結果
連立1階常微分方程式
2個の未知関数$x_0(t), x_1(t)$に関する1階の連立常微分方程式
$$ \begin{cases} x_0' = x_0 - 2 x_1 \\ x_1' = 2 x_0 - 1.5 x_1 \end{cases} $$
を考える。
この問題の解の時刻推移を計算するコードは以下のようになる。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
dt = 0.1 # サンプル周期
times = np.arange(0, 20+dt, dt)
x_history = [[2, -2]] # xの時刻歴データ
x = ca.MX.sym('x',2); # Two states
rhs = ca.vertcat(x[0]-2*x[1], 2*x[0]-1.5*x[1])
ode = {'x': x,
'ode': rhs}
opts = {'t0':0,
'tf':dt}
F = ca.integrator('F', 'cvodes', ode, opts)
for t in times[:-1]:
res = F(x0=x_history[-1])
x_history += [res['xf'].toarray().flatten().tolist()]
fig, ax = plt.subplots()
ax.plot(times, x_history)
ax.legend(['x0', 'x1'])
ax.set_xlabel('t')
ax.set_ylabel('x0, x1')
ax.grid()
plt.show()
|
未知関数の数が2つになるため、x, rhsをベクトルとした。
実行すると、以下のグラフが出力される。
参考
CasADiの公式リファレンス
