はじめに #
2クラス分類モデルの評価指標としてよく用いられる、混同行列、F値、ROC曲線、AUCについて解説します。また、PythonとScikit-learnによる評価指標の計算方法も示します。実行環境は以下の通りです。
- Python: 3.9.7
- NumPy: 1.20.3
- sklearn: 0.24.2
混同行列 #
混同行列 (confusion matrix) は2クラス分類の予測結果を整理するためによく使われます。ある分類モデルを使って、正解が分かっているデータに対して予測を行ったとします。ここで、片方のクラスを正、もう片方のクラスを負とします。混同行列はこの予測結果のデータ数を以下の表のようにまとめたものです。各行は予測されたクラス、各列は本当のクラスになります。
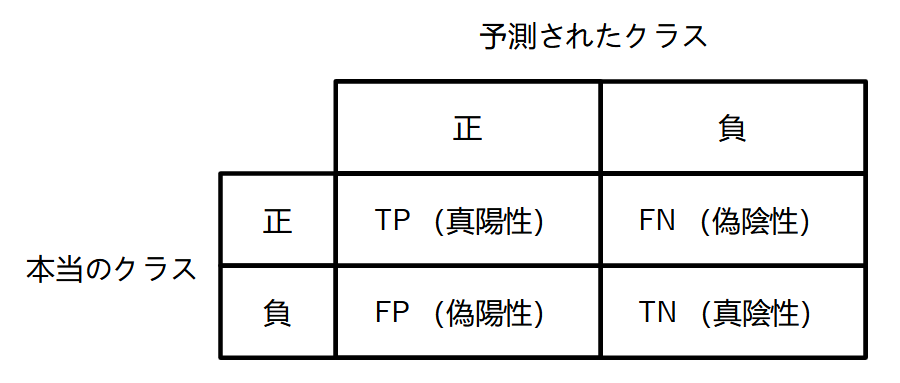
混同行列の各要素の詳細を以下に示します。
- TP(true positive, 真陽性): 正のクラスのデータを正しく予測できた数
- FN(false negative, 偽陰性): 正のクラスのデータを間違って負と予測した数
- FP(false positive, 偽陽性): 負のクラスのデータを間違って正と予測した数
- TN(true negative, 真陰性): 負のクラスのデータを正しく予測できた数
もし分類モデルが完璧であれば、FNとFPの値は0になります。
混同行列を使うと、分類モデルの正しい予測の割合、すなわち正解率 (accuracy) は次式で計算されます。
$$ \mathrm{accuracy} = \frac{TP+TN}{TP+FN+FP+TN} $$ただし、正解率は直感的に理解しやすいですが、クラスによってデータ数が偏っている場合は不適切です。例えば100個のデータの内、正のクラスのデータが90個を占める場合を考えます。常に正のクラスを予測として返す分類モデルがあるとすると、その正解率は
$$ \frac{TP+TN}{TP+FN+FP+TN} = \frac{90+0}{90+0+10+0} = 0.9 $$すなわち、90%と非常に高い数値になってしまいます。
そこで、分類モデルをより正確に評価できる指標として、適合率 (precision) と再現率 (recall) が合わせて用いられます。適合率は正の予測に対する正解率で、次式で計算されます。
$$ \mathrm{precision} = \frac{TP}{TP+FP} $$一方、再現率は正しく分類された正データの割合です。
$$ \mathrm{recall} = \frac{TP}{TP+FN} $$scikit-learnの混同行列・適合率・再現率 #
scikit-learnには、混同行列・適合率・再現率が実装されています。
- 混同行列:
sklearn.metrics.confusion_matrix(y_true, y_pred) - 適合率:
sklearn.metrics.precision_score(y_true, y_pred) - 再現率:
sklearn.metrics.recall_score(y_true, y_pred)
y_trueは正解データ、y_predは予測データです。使用例を以下に示します。
import numpy as np
from sklearn.metrics import confusion_matrix, precision_score, recall_score
y_true = np.array([0, 0, 0, 0, 0, 1, 1, 1]) # 正解データ
y_pred = np.array([0, 0, 0, 1, 1, 0, 1, 1]) # 予測データ
print(confusion_matrix(y_true, y_pred))
# [[3 2]
# [1 2]]
print(precision_score(y_true, y_pred))
# 0.5
print(recall_score(y_true, y_pred))
# 0.6666666666666666
F値 #
F値 (F1score) は適合率と再現率を1つの指標としてまとめたものです。2つ以上の分類モデルを比較する場合などに用いられます。
F値は適合率と再現率の調和平均をとったものです。調和平均は広義の平均であり、低い値に大きな重みづけを与えます。そのため、適合率と再現率の両方が大きくなければ、F値は大きくなりません。また、F値は0から1までの値を取ります。
$$ F_1 = \frac{2}{ (\mathrm{precision})^{-1} + (\mathrm{recall})^{-1} } = \frac{TP}{TP + \frac{1}{2}(FN + FP)} $$scikit-learnのF値 #
scikit-learnにはF値が実装されています。
sklearn.metrics.f1_score(y_true, y_pred)
y_trueは正解データ、y_predは予測データです。使用例を以下に示します。
import numpy as np
from sklearn.metrics import f1_score
y_true = np.array([0, 0, 0, 0, 0, 1, 1, 1])
y_pred = np.array([0, 0, 0, 1, 1, 0, 1, 1])
print(f1_score(y_true, y_pred))
# 0.5714285714285715
ROC曲線 #
2クラス分類の評価には、ROC曲線 (Receiver Operating Characteristic curve) もよく用いられます。ROC曲線は、クラスの分類結果を0~1の間の連続値として出力する分類モデルを評価できる指標であり、偽陽性率と真陽性率をプロットした曲線です。
偽陽性率は負のクラスの内、誤って正と予測されたデータの割合です。また、真陽性率は正のクラスの内、正しく正と予測されたデータの割合です。混同行列の要素を使うと次式で計算されます。
偽陽性率:\(FP/(FP+TN)\)
真陽性率:\(TP/(TP+FN)\)
偽陽性率と真陽性率は、クラスによるデータ数の偏りの影響を受けません。そのため、ROC曲線も偏りの影響を受けない指標です。
次に、ROC曲線の具体例を示します。5個のデータに対して、ある分類モデルの予測値が以下のように得られたとします。ここで、予測値は大きいほど正のクラスである可能性が高い値となります。予測値に対する閾値をここでは0.5として、予測値が0.5以上を正、0.5未満を負に分類します。このとき、予測されたクラスは表の右端の列のようになります。
| データNo. | 本当のクラス | 予測値 | 予測されたクラス |
|---|---|---|---|
| 1 | 正 | 0.8 | 正 |
| 2 | 正 | 0.4 | 負 |
| 3 | 正 | 0.3 | 負 |
| 4 | 負 | 0.7 | 正 |
| 5 | 負 | 0.1 | 負 |
予測結果に対して、混同行列と偽陽性率、真陽性率は以下になります。
| 正と予測 | 負と予測 | |
|---|---|---|
| 本当は正 | TP: 1 | FN: 2 |
| 本当は負 | FP: 1 | TN: 1 |
偽陽性率:\(FP/(FP+TN)=1/(1+1)=0.5\)
真陽性率:\(TP/(TP+FN)=1/(1+2)=0.333\)
これで、偽陽性率と真陽性率の1組の値が得られました。同様に、閾値の値を0から1まで変化させて、偽陽性率と真陽性率の値をそれぞれ求めます。得られた値をプロットするとROC曲線(下図の青色の線)になります。ここで、真陽性率は高い方が望ましく、偽陽性率は低い方が望ましいことに注意します。閾値を小さくすると真陽性率と偽陽性率はともに1に近づきます。一方で、閾値を大きくすると、真陽性率と偽陽性率はともに0に近づくトレードオフの関係にあります。
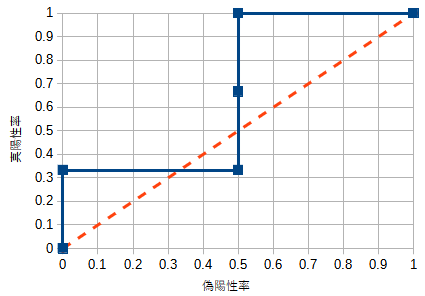
性能が良い分類モデルでは、ROC曲線はグラフの左上に近づきます。一方で、完全にランダムな予測値を返す分類モデルでは、ROC曲線はグラフの左下から右上を結ぶ直線(グラフのオレンジ色の破線)になります。すなわち、ROC曲線の下側の面積が大きいほど、優れた分類モデルと言えます。この面積をAUC (area under the curve) と呼びます。AUCの最大値は1で、これに近いほど優れた分類モデルです。
