SciPyを使ったFIRフィルタによる波形整形

はじめに

SciPyを使って、FIR (Finite Impulse Response, 有限インパルス応答) フィルタによる離散信号の波形を整形する。ローパス、ハイパス、バンドパス、バンドエリミネイトの各フィルタの設計から、信号への適用まで行う。

環境

ソフトウェア	バージョン
Python	3.6.5
NumPy	1.14.2
SciPy	1.0.1

元の離散信号

次の3つの信号を合成して、フーリエ変換を行う離散信号とする。

周波数30[Hz], 振幅3の正弦波
周波数50[Hz], 振幅0.3の正弦波
周波数120[Hz], 振幅0.2の正弦波

信号のデータ点数は2048, サンプリング周期は0.001[s]とする。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

N = 1024            # サンプル数
dt = 0.001          # サンプリング周期 [s]
f1, f2, f3 = 10, 60, 300 # 周波数 [Hz]

t = np.arange(0, N*dt, dt) # 時間 [s]
x = 3*np.sin(2*np.pi*f1*t) + 0.3*np.sin(2*np.pi*f2*t) + 0.2*np.sin(2*np.pi*f3*t) # 信号

SciPyの関数

フィルタの設計

まず、関数scipy.signal.firwin()によりフィルタを設計する。

1
2
3


scipy.signal.firwin(numtaps, cutoff, width=None, 
                    window='hamming', pass_zero=True, 
                    scale=True, nyq=None, fs=None)

主な引数の説明は以下の通り。

numtaps: int
FIRフィルタの長さ。

cutoff: float or 1D array_like
カットオフ周波数。
ローパス、ハイパスの場合はfloat,
バンドパス、バンドエリミネイトの場合は1D array_likeとする。
cutoffは0からfs/2の間にしなければならない。

window: string
窓関数を指定する。デフォルトは’hamming' （ハミング窓）。

pass_zero: bool
周波数0（直流成分）が通過するか指定。
デフォルトはTrue.

fs: float
信号のサンプル周波数。デフォルト値は2.

scipy.signal.firwin()の戻り値は、長さnumtapsのFIRフィルタの係数配列となる。

フィルタの適用

次に、関数scipy.signal.lfilter()により信号にフィルタを適用する。

1

scipy.signal.lfilter(b, a, x, axis=-1, zi=None)

主な引数の説明は以下の通り。

b: array
分子の係数。

a: array
分母の係数。

x: array
入力信号。

戻り値は、フィルタを掛けた信号の配列となる。

この関数では、フィルタが以下の式で表されているものとする。
$$ H(z)=\frac{\sum_{k=0}^{M} b_k z^{-k} } {\sum_{k=0}^{N} a_k z^{-k} } $$
引数bが右辺の分子の係数、引数aが右辺の分母の係数に対応する。今回はFIRフィルタを扱うので、分母のaを1とおく。

波形整形

基本的なフィルタを信号に適用して、波形や振幅の変化を確認する。

ローパスフィルタ

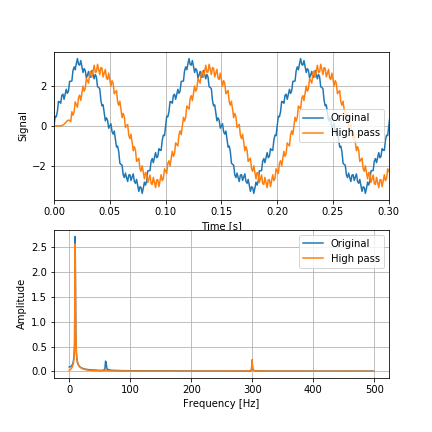
カットオフ周波数を40[Hz]としたローパスフィルタ。

1
2
3
4
5


filter1 = signal.firwin(numtaps=21, cutoff=40, fs=1/dt)
y1 = signal.lfilter(filter1, 1, x)

F1 = np.fft.fft(y1)
Amp1 = np.abs(F1/(N/2))

60, 300[Hz]の高周波成分が減衰・除去されている。
low_pass

ハイパスフィルタ

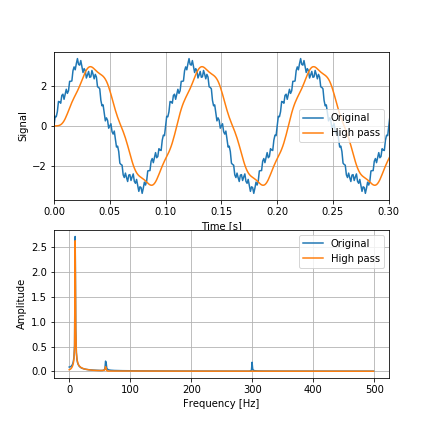
カットオフ周波数を100[Hz]としたハイパスフィルタ。

1
2
3
4
5


filter2 = signal.firwin(numtaps=51, cutoff=100, fs=1/dt, pass_zero=False)
y2 = signal.lfilter(filter2, 1, x)

F2 = np.fft.fft(y2)
Amp2 = np.abs(F2/(N/2))

10, 60[Hz]の低周波成分が除去されている。
high_pass

バンドパスフィルタ

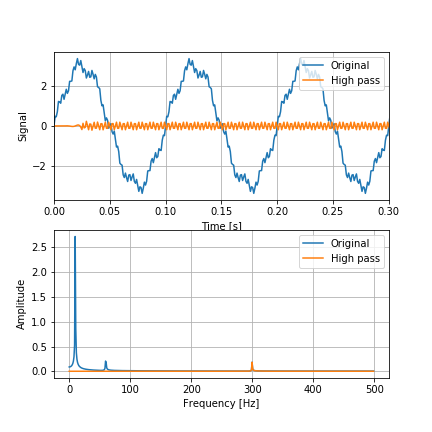
通過周波数を30～100[Hz]としたバンドパスフィルタ。

1
2
3
4
5


filter3 = signal.firwin(numtaps=51, cutoff=[30, 100], fs=1/dt, pass_zero=False)
y3 = signal.lfilter(filter3, 1, x)

F3 = np.fft.fft(y3)
Amp3 = np.abs(F3/(N/2))

10, 300[Hz]の信号が減衰・除去されいている。
band_pass

バンドエリミネイトフィルタ

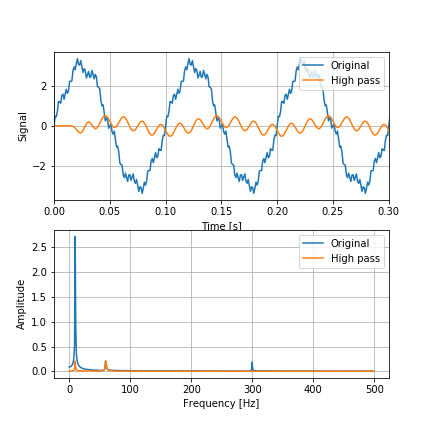
通過周波数を30[Hz]以下、100[Hz]以上としたバンドエリミネイトフィルタ。

1
2
3
4
5


filter4 = signal.firwin(numtaps=31, cutoff=[30, 100], fs=1/dt)
y4 = signal.lfilter(filter4, 1, x)

F4 = np.fft.fft(y4)
Amp4 = np.abs(F4/(N/2))