ナップサック問題と分枝限定法

※記事内に商品プロモーションを含むことがあります。

はじめに

最適化問題には、最適な組み合わせを選ぶ問題がある。このような組み合わせ最適化問題は、問題の規模が大きくなると、連続値の中から最適な値を見つける問題と比べて、解きづらくなる性質がある。

組み合わせ最適化問題を効率的に解く手法として、分枝限定法と呼ばれる手法がある。分枝限定法は、組み合わせの条件を連続値に緩和した問題（緩和問題）を解いて、上界と下界を用いて無駄な探索を省略する手法である。

本記事では、はじめに組合せ最適化問題の1つである0-1ナップサック問題について簡単に示す。次に、分枝限定法のアルゴリズムを示し、0-1ナップサック問題を対象とした分枝限定法の例題を示す。さらに、分枝限定法を実装した無償ソルバ、および例題を検証するためのPythonソースコードを示す。

ソースコードの検証環境

	バージョン
Python	3.7.4
Pyomo	5.6.9
GLPK	4.65

リンク

ナップサック問題

ナップサック問題とは、次のような組合せ最適化問題である。

N種類の荷物があり、各荷物は価値$p_i$と容積$c_i$を持つ($i=1,…,N$)。
また、ナップサックの容量を$C$とする。
ナップサックの容量を超えない範囲で荷物を詰めるときに、
詰める荷物の価値を最大にするには、どのような荷物の組み合わせとすればよいか。

同じ種類の荷物は1つまでしか入れられない場合や、いくつでも入れられる場合など、いくつかのバリエーションがある。前者の場合を特に0-1ナップサック問題と呼ぶ。本記事では0-1ナップサック問題を対象に分枝限定法について述べる。

0-1ナップサック問題を式で表すと、以下のようになる。

$$ \begin{array}{ll} \text{maximize} \ & \sum_{i=1}^{N} p_i x_i \\ \text{subject to} \ & \sum_{i=1}^{N} c_i x_i \le C \\ & x_i \in \{0, 1\}, (i=1, …, N) \end{array} $$

ここで、$x_i=0$は荷物$i$がナップサックに詰められていないことを表し、$x_i=1$は荷物$i$がナップサックに詰められていることを表す。

0-1ナップサック問題の最適解を総当たりで求めようとすると、$2^N$回の計算が必要になり、$N$が大きくなるにつれて計算時間が指数関数的に増加してしまう。

分枝限定法

分枝限定法 (branch and bound) は、変数$x_i$の整数条件を連続値に緩和した問題（緩和問題）を解いて、上界と下界を用いて無駄な探索を省略する手法である。（緩和問題が単純な線形計画問題である場合、大規模な問題であったとしても比較的容易に最適解が求められることが、分枝限定法の前提にある）

通常、緩和問題の最適解は元の整数計画問題の最適解と一致しない(0, 1の組み合わせにならない)ので、連続値に緩和した変数を1つずつ0または1に固定して、問題を分割させながら探索する。この分割操作を分枝 (branching) と呼ぶ。

さらに、分枝限定法の場合、上界 (upper bound) とは緩和問題の最適値であり、元の整数計画問題の最適値か、それより大きいとみなせる値である。また、下界 (lower bound) とは元の整数計画問題の最適値かそれより小さいとみなせる値である。（上界）≥（最適値）≥（下界）の関係が成り立つ。

したがって、ある分枝における下界が、別の分枝における上界よりも大きい場合、後者の分枝をそれ以上探索しても、最適解が得られる見込みがないため、探索を打ち切る。この打ち切り操作を限定 (bounding) 操作と呼ぶ。

分枝限定法の例

次の0-1ナップサック問題(N=4)を対象に、分枝限定法の例を示す。

$$ \begin{array}{ll} \text{maximize} \ & 2x_1 + 4x_2 + 20x_3 + 24x_4 \\ \text{subject to} \ & x_1 + 4x_2 + 5x_3 + 8x_4 \le 9 \\ & x_i \in \{0, 1\}, (i=1, …, 4) \end{array} $$

まず、$x_i (i=1,…,4)$を全て連続値とした緩和問題(P0)を考える。緩和問題P0は、$\boldsymbol{x} =(0, 0, 1, 0.5)$で最適解32をとる。この32という値は整数条件を緩めて得られた解であるから、元の整数計画問題の解は32以下であると考えられる（すなわち、32は上界である）。

次に、緩和問題P0の最適解において整数でなかった$x_4$が、0の場合と1の場合に分けて考える（分枝）。$x_4=0$で固定として$x_1, x_2, x_3$を連続値とした緩和問題をP1, $x_4=1$で固定として$x_1, x_2, x_3$を連続値とした緩和問題をP2とする。

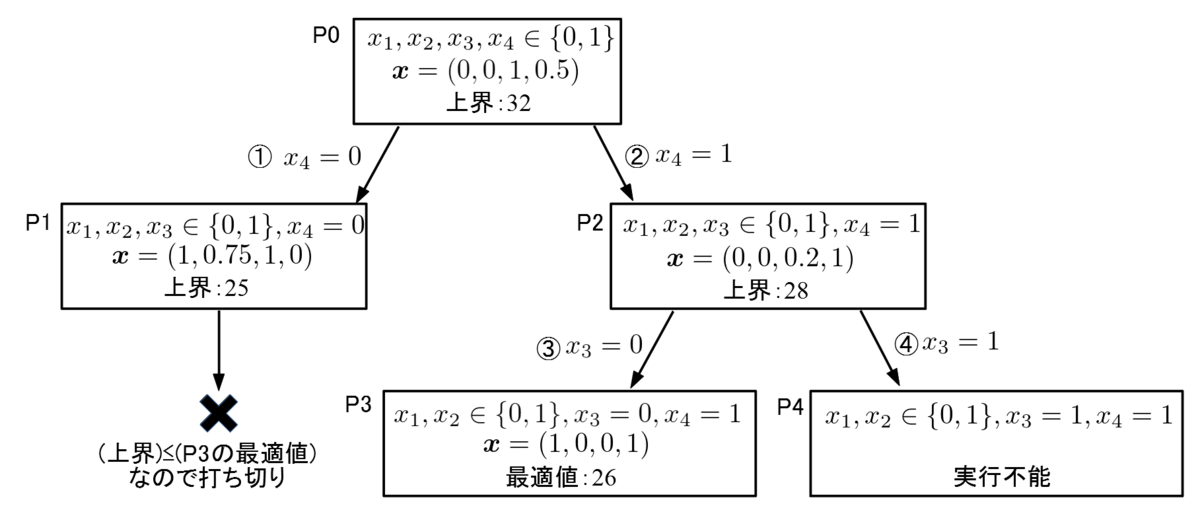
$0-1ナップサック問題への分枝限定法の適用例$

緩和問題P1を解くと、$\boldsymbol{x} =(1, 0.75, 1, 0)$で最適値25をとる。P1の上界は25である。

また、緩和問題P2は、$\boldsymbol{x} =(0, 0, 0.2, 1)$で最適値28をとる。P2の上界は28である。

P1とP2のどちらを先に探索しても良いが、ここでは上界が大きいP2 (28 > 25) に整数計画問題の最適解がある可能性が高いと考え、P2を先に探索する。この探索方法を最良優先探索と呼ぶ。

P2の最適解$\boldsymbol{x} =(0, 0, 0.2, 1)$において、整数でないのは$x_3=0.2$である。P2をさらに分枝して、
$(x_3, x_4)=(0, 1)$で固定として$x_1, x_2$を連続値とした緩和問題をP3,
$(x_3, x_4)=(1, 1)$で固定として$x_1, x_2$を連続値とした緩和問題をP4とする。

P3を解くと、$\boldsymbol{x} =(1, 0, 0, 1)$で最適値26をとる。この解は全て整数であるので、元の整数計画問題の解の候補となる。また、元の整数計画問題の解は、P3の最適値26以上と考えられるため、この26は下界である。また、P3において、$x_1, x_2$をさらに0または1に固定したとしても、P3より良い解が得られることはないため、これ以上の分枝は不要である。

ここで、緩和問題P1の上界は25であった。これは、P1の連続値を整数に縛った場合、その最適値は25以下であることを意味する。すなわち、P1を分枝しても、P3の下界26より良い解が得られる可能性がないことを意味するため、P1の探索を打ち切る（限定操作）。

最後に、緩和問題P4は$(x_3, x_4)=(1, 1)$とした時点で、制約条件$x_1 + 4x_2 + 5x_3 + 8x_4 \le 9$を満たさず実行可能解を持たないため、これ以上分枝する必要はない。

以上が分枝限定法の例である。全ての解候補を探索することなく、効率的に大域的最適解を求められることが分かる。

なお、最良優先探索以外にも様々な探索アルゴリズムがあり、深さ優先探索という手法も良く使われる。深さ優先探索は、上記の例で示すとP1を解いた後、P2より先にP1を分枝して次々解いていく方法であり、以下のメリットがある。

実装が簡単
使用メモリが少なくて済む
早く暫定解が得られる

一方、最良優先探索と比べると、計算量が多くなりやすいデメリットがある。

分枝限定法が実装されている無償ソルバ

分枝限定法が実装されている主な無償ソルバは以下の通り。

CBC (COIN-OR branch and cut)
GLPK (GNU Linear Programming Kit)

GLPKはconda環境でインストールでき、pyomoというモデリングツールとの連携も容易である。

検証用のPythonコード

上記の分枝限定法の例を検証したPythonのソースコードを以下に示す。PyomoとGLPKを使用した。両者の導入については、以下の記事を参照。
Pyomoで線形計画問題を解く

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


import pyomo.environ as pyo

def ObjRule(model):
    return 2*model.x1 + 4*model.x2 + 20*model.x3 + 24*model.x4

def ConstRule(model):
    return 1*model.x1 + 4*model.x2 + 5*model.x3 + 8*model.x4 <= 9

model = pyo.ConcreteModel()
model.x1 = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0, 1))
model.x2 = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0, 1))
model.x3 = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0, 1))
model.x4 = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0, 1))
# boundsの範囲を(0, 0)や(1, 1)とすれば値を固定できる

model.OBJ = pyo.Objective(rule = ObjRule,
                          sense = pyo.maximize)

model.Constraint1 = pyo.Constraint(rule = ConstRule)

opt = pyo.SolverFactory('glpk')

res = opt.solve(model, tee=False) # tee=Trueとすればソルバーのメッセージが表示

print(f"評価関数：{model.OBJ()}")
print(f"x1: {model.x1()}")
print(f"x2: {model.x2()}")
print(f"x3: {model.x3()}")
print(f"x4: {model.x4()}")

また、変数x1, …, x4を以下のように置き換えれば、整数計画問題としてGLPKに解かせることができる。

1
2
3
4


model.x1 = pyo.Var(domain=pyo.Binary)
model.x2 = pyo.Var(domain=pyo.Binary)
model.x3 = pyo.Var(domain=pyo.Binary)
model.x4 = pyo.Var(domain=pyo.Binary)

参考

ナップサック問題について
ナップサック問題 - Wikipedia

分枝限定法について
数理計画法第6回（東北大学講義資料、PDF）
最適化手法第 5回整数計画法 (4)：分枝限定法（電通大講義資料、PDF）