※記事内に商品プロモーションを含むことがあります。

はじめに

関数の2階微分を利用する最適化手法であるニュートン法について、機械学習プロフェッショナルシリーズの「機械学習のための連続最適化」で勉強したので、備忘録として残す。

本記事では、ニュートン法と、簡単な関数を対象にPythonで実装した例を示す。使用したPythonとライブラリのバージョンは以下の通り。

ニュートン法

ニュートン法は、関数の2階微分までの情報を用いる最適化手法である。1階微分の情報までしか用いない再急降下法（以下の記事を参照）と比較すると、ニュートン法は解の収束速度が速い利点がある。
直線探索を使った最急降下法をPythonで実装

最小化したい関数$f(\boldsymbol{x})$が2回連続微分可能であるとする。また、反復法により得られた$k$回目の解を$\boldsymbol{x_k}$とし、$\boldsymbol{x_k}$に対する解の更新ベクトルを$\boldsymbol{d}$とする。このとき、更新後の解$\boldsymbol{x_k+d}$における2次のテイラー展開は次式で近似される。

$$ f(\boldsymbol{x_k+d}) = f(\boldsymbol{x_k}) + \nabla f(\boldsymbol{x_k})^\top \boldsymbol{d} + \frac{1}{2} \boldsymbol{d}^\top \nabla ^2 f(\boldsymbol{x_k}) \boldsymbol{d} $$

ここで、$\boldsymbol{x_k+d}$が最適解と仮定すると、$f(\boldsymbol{x_k+d})$を微分した勾配ベクトルは$\boldsymbol{0}$である。すなわち、

$$ \nabla f(\boldsymbol{x_k})^\top + \nabla ^2 f(\boldsymbol{x_k}) \boldsymbol{d} = 0 $$

ここで、ヘッセ行列$\nabla ^2 f(\boldsymbol{x_k})$が正定値行列とする。
正定値行列とは、任意のベクトル$\boldsymbol{x}$≠$0$に対して、
$ \boldsymbol{x}^\top A \boldsymbol{x} > 0 $
となる行列$A$のことである。また、対称行列$A$が正定値行列の場合、$A$は正則であり、逆行列を持つ。

すなわち、ヘッセ行列は対称行列であるから、正定値行列であれば逆行列を持つ。
先ほどの式を$\boldsymbol{d}$について解くと、以下のようになる。

$$ \boldsymbol{d} = - (\nabla ^2 f(\boldsymbol{x_k}))^{-1} \nabla f(\boldsymbol{x_k}) $$

したがって、解を以下のように更新すれば、関数値が減少することが期待できる。

$$ \begin{array}{ll} \boldsymbol{x_{k+1}} & = \boldsymbol{x_k} + \boldsymbol{d} \\ & = \boldsymbol{x_k} - (\nabla ^2 f(\boldsymbol{x_k}))^{-1} \nabla f(\boldsymbol{x_k}) \end{array} $$

条件を満たすまで解の更新を繰り返す。
以上がニュートン法のアルゴリズムである。

ニュートン法の実装例

以下の目的関数を考える。
$$ f(\boldsymbol{x}) = x_1^4 + x_1^2 + x_1 x_2 + x_2^2 + 2 x_2^4 $$

ただし、$\boldsymbol{x}=[x_1, x_2 ]$ である。関数を図示すると以下のようになる。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

N = 41
x1 = np.linspace(-2, 2, N)
x2 = np.linspace(-2, 2, N)

X1, X2 = np.meshgrid(x1, x2)
Y = X1**4 + X1**2 + X1*X2 + X2**2 + 2*X2**4

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(X1, X2, Y, cmap='bwr', linewidth=0)
fig.colorbar(surf)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
fig.show()

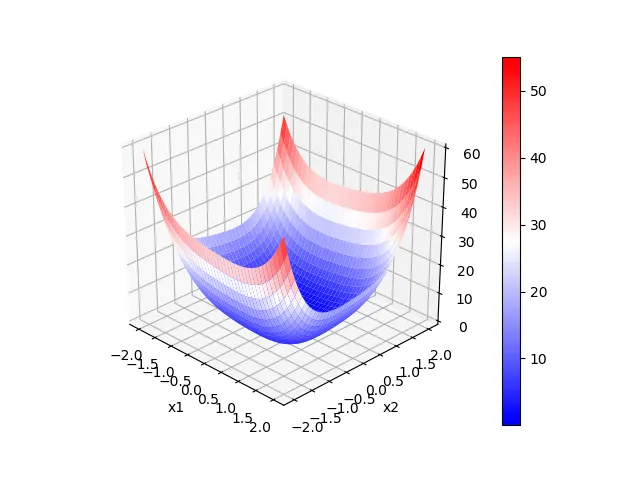
目的関数$f(\boldsymbol{x})$は、$(x_1, x_2)=(0, 0)$で最小値0をとる。
また、関数の勾配ベクトルとヘッセ行列はそれぞれ以下のようになる。

$$ \nabla f(\boldsymbol{x}) = [4x_1^3 + 2x_1 + x_2, x_1+ 2x_2 + 8x_2^3 ]^{\top} $$

$$ \nabla ^2 f(\boldsymbol{x}) = \begin{bmatrix} 12x_1^2 + 2 & 1 \\ 1 & 2+24x_2^2 \end{bmatrix} $$

関数値と勾配ベクトル、ヘッセ行列を返す関数を以下のように定義する。

1
2
3
4
5
6
7

def f(x0, x1):
    y = x0**4 + x0**2 + x0*x1 + x1**2 + 2*x1**4
    dydx = np.array([4*x0**3 + 2*x0 + x1,
                     x0 + 2*x1 + 8*x1**3])
    H = np.array([[12*x0+2, 1],
                  [1, 2+24*x1**2]])
    return y, dydx, H

ニュートン法を用いた関数の最小化のコードは以下のようになる。ここでは、初期値を$(x_1, x_2)=(2, 2)$とし、反復回数を9回とした。

1
2
3
4
5
6
7
8

x0, x1 = 2, 2
print("i    x1          x2           f(x)")
for i in range(10):    
    y, dydx, H = f(x0, x1)
    print(f"{i:3d} [{x0:10.3e}, {x1:10.3e}], {y:10.3e}")
    d = - np.dot(np.linalg.inv(H), dydx)
    x0 += d[0]
    x1 += d[1]

結果: ニュートン法による最適化計算の推移を以下に示す。$(x_1, x_2)=(0, 0)$で最小値0に収束しており、最適解を求められたことが分かる。

i    x1          x2           f(x)
  0 [ 2.000e+00,  2.000e+00],  6.000e+01
  1 [ 5.654e-01,  1.300e+00],  8.566e+00
  2 [ 2.610e-01,  8.201e-01],  1.864e+00
  3 [ 5.120e-02,  4.836e-01],  3.707e-01
  4 [-8.328e-02,  2.486e-01],  5.574e-02
  5 [ 2.092e-02,  6.459e-02],  5.997e-03
  6 [ 1.783e-03,  1.204e-03],  6.775e-06
  7 [ 2.504e-05, -1.251e-05],  4.703e-10
  8 [ 5.015e-09, -2.508e-09],  1.887e-17
  9 [ 2.012e-16, -1.006e-16],  3.037e-32

参考

ニュートン法のアルゴリズムについて、機械学習プロフェッショナルシリーズの「機械学習のための連続最適化」を参考にさせて頂いた。

また、記事では触れなかったが、ニュートン法による探索方向は降下方向とは異なる場合があるため、初期値が局所解から離れていると収束しない場合がある。
その欠点を補うため、探索方向が降下方向となるようにニュートン法を改良した修正ニュートン法と呼ばれる手法があり、同書籍で紹介されている。