PyomoとCouenneで非凸の混合整数非線形計画問題(MINLP)を解く

※記事内に商品プロモーションを含むことがあります。

はじめに

PyomoはPythonで書かれた最適化モデリングツールである。一般に、高速な最適化ソルバはC言語などで書かれており、最適化問題をAMPLなどのフォーマットで記述する必要がある。そのため、最適化モデリングツールを使って、（Pythonなど）他の言語で記述された問題を変換して最適化ソルバに渡す。

また、Couenneは非凸なMINLP問題を解くことができる最適化ソルバである（詳細は後述）。MINLPは混合整数非線形計画問題 (Mixed Integer Nonlinear Programming) の略である。PyomoからCouenneを呼び出して使用することができる。

本記事では、Couenneの紹介、およびWindowsにおける導入方法、PyomoとCouenneを用いてMINLP問題を解く例を示す。

また、Pyomoは既に導入されているものとする。Pyomoの導入方法と基本的な使い方は以下の記事を参照。
Pyomoで線形計画問題を解く

環境

Windows 10 Home
Couenne Ver. 0.3.2

リンク

Couenneの基本

Couenne (Convex Over and Under ENvelopes for Nonlinear Estimation) は、非凸なMINLPを解くことができるソルバである。Couenneには、spatial branch & bound（日本語訳は不明だが、空間分枝限定法？）と呼ばれる最適化手法が実装されている。

なお、Couenneは同じCOIN-ORプロジェクトで開発された以下の最適化ソルバを間接的に呼び出して使用している。

CBC: MILPソルバ
CLP: LPソルバ（CBCから使用される）
IPOPT: NLPソルバ

Coueeneの導入

Couenneを使用するには、以下の2つの方法がある。

ネットから実行ファイルをダウンロードして使う
ソースコードをビルドして使う

Windowsで2の方法を取るには、Cygwinを導入したり、BlasやLapackなどのライブラリを用意する必要があるなどハードルが高いので、ここでは1の方法を取る。

まず、以下のページの"Couenne-0.3.2-win32-..>“からzipファイルをダウンロードする。
https://www.coin-or.org/download/binary/Couenne/

ただし、2011年から実行ファイルの配布が止まっており、バージョン0.3.2までしか入手できない。最新のバージョンを利用する場合は、ソースコードをビルドする必要がある。

ダウンロードしたzipファイルを解凍すると、binフォルダの中にcouenne.exeがある。この実行ファイルには、Couenneが呼び出すライブラリが全て含まれている。

次に、Pyomoからcouenne.exeを呼ぶためにパスを通す。具体的には以下のような方法がある。

Windowsの環境変数のPathにcouenne.exeがあるフォルダを追加する
Pythonのカレントディレクトリにcouenne.exeを置く

以上でPyomoからCouenneを使用する準備が整った。

なお、binフォルダに含まれるbonmin.exe, cbc.exe, ipopt.exeも、couenne.exeと同様にパスを通せばPyomoから呼び出して使用することができる。

非凸MINLPの例題

以下の2変数の非凸MINLPを考える。

$$ \begin{array}{ll} \text{minimize} & 3 x_1^4 - 4 x_1^3 -12 x_1^2 + 3 x_2^4 - 4 x_2^3 -12 x_2^2 \\ \text{subject to} & -5 \le x_1 \le 5, -5 \le x_2 \le 5 \\ & x_1, x_2 \in \mathbb{Z} \end{array} $$

ここで、$\mathbb{Z}$は整数の集合を表す。また、$x_1, x_2$が実数の場合の-2～3付近を拡大したグラフを示す。

pyomo-couenne

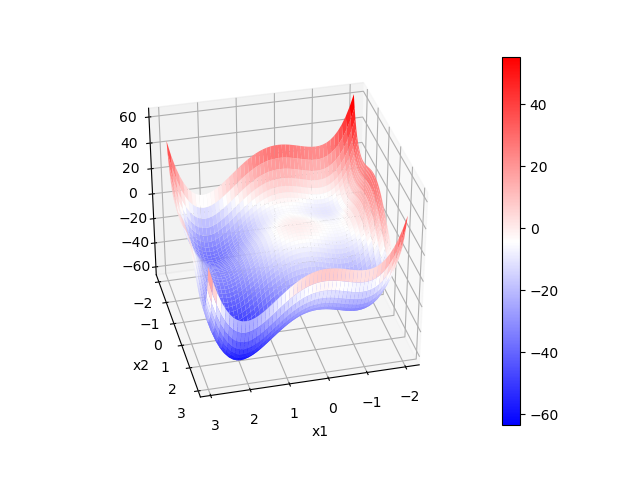
$(x_1, x_2)=(2, 2)$で大域的最適解$-64$を持つが、$(x_1, x_2)=(-1, -1), (-1, 2), (2, -1)$の3箇所で局所解を持つ非凸な問題である。

Pyomoのソースコード

上記の問題をPyomoとCouenneで解くためのコードは以下の通り。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


import pyomo.environ as pyo

def ObjRule(m):
    return 3*m.x1**4-4*m.x1**3-12*m.x1**2 + 3*m.x2**4-4*m.x2**3-12*m.x2**2

model = pyo.ConcreteModel(name="Nonconvex MINLP sample")

model.x1 = pyo.Var(domain=pyo.Integers, bounds=(-5, 5), initialize=-1)
model.x2 = pyo.Var(domain=pyo.Integers, bounds=(-5, 5), initialize=-1)

model.OBJ = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize)

opt = pyo.SolverFactory('couenne')
res = opt.solve(model, tee=False)
# tee=Trueとすればソルバーのメッセージが表示

print(f"評価関数：{model.OBJ()}")
print(f"x1: {model.x1()}")
print(f"x2: {model.x2()}")

ここでは、変数の初期値をあえて局所解とした。

実行結果

コードを実行すると以下が表示され、大域的最適解を得られたことが分かる。

1
2
3


評価関数：-64.0
x1: 2.0
x2: 2.0

Coueeneのオプション

Coueeneにオプションを指定する場合、カレントディレクトリにcouenne.optという設定ファイルを置く。一例を以下に示す。

# ログの詳細度
problem_print_level 6

# 許容誤差
feas_tolerance 1e-6

# 計算時間の制限
time_limit 10

オプションのキーワードと値を半角スペースで区切って記述する。また、#以降にコメントを記述できる。

なお、なぜかPyomoのソースコードからオプションを指定することはできなかった。

1
2


opt = pyo.SolverFactory('couenne')
opt.options["problem_print_level"] = 5

実行結果

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


couenne: Unknown keyword "problem_print_level"
Unknown keyword "problem_print_level"
ERROR: Solver (asl) returned non-zero return code (1)
ERROR: See the solver log above for diagnostic information.
Traceback (most recent call last):

  File "D:\document\Python Scripts\pyomo_couenne\pyomo_couenne.py", line 27, in <module>
    res = opt.solve(model, tee=True)

  File "C:\Users\ABC\Anaconda3\lib\site-packages\pyomo\opt\base\solvers.py", line 596, in solve
    raise ApplicationError(

ApplicationError: Solver (asl) did not exit normally

参考文献

CouenneのGitHubリポジトリ
COIN-OR Foundation - Couenne

Couenneのユーザマニュアル（オプションについて記載）
COUENNE: a user’s manual (PDF)