はじめに
Pythonと最適化ライブラリCasADiを使って、Direct Multiple Shooting法と呼ばれる手法によって最適制御問題を解きました。対象とした例題は、2次元平面上を移動する物体の移動経路です。指定の位置に物体を到達させる入力と軌道を求めます。
Direct Multiple Shooting法は以下の特徴を持つ最適制御手法です。
- 制御の開始から終了まで、時刻を$t_0, t_1, …, t_f$と（等間隔に）分割する
- 分割された時間幅ごとに、入力$u(t)$に対するシミュレーションを行う
- 時間幅の最後の状態変数が次の時間幅の初期状態と一致する制約を設ける
CasADiに関する詳細は以下の記事を参考にしてください。
CasADiとIPOPTで非線形計画問題を解く – Helve Tech Blog
PythonとCasADiで常微分方程式を解く – Helve Tech Blog
この記事で使用したPythonとライブラリのバージョンは以下の通りです。
| ソフトウェア |
バージョン |
| Python |
3.9.7 |
| NumPy |
1.20.3 |
| Pandas |
1.3.4 |
| CasADi |
3.5.5 |
| IPOPT |
3.12.3 |
| Matplotlib |
3.4.3 |
CasADiとIPOPTがインストールされていない場合、以下でインストールします。
pip install casadi
pip install ipopt
2次元平面上を移動する物体の運動方程式
まず、対象とする問題を示します。2次元平面上の物体に力を加えて移動させる単純な問題です。摩擦は考えないものとします。物体の質量を$m$とします。$x$軸と$y$軸方向の物体の位置を$x, y$とし、制御入力（作用させる力）を$F_x, F_y$とすると、運動方程式は以下になります。
$$m \ddot{x} = F_x \\ m \ddot{y} = F_y$$
次に、CasADiで運動方程式を扱えるように、$\dot{z}=f(z)$という1階微分方程式の形に式を変形します。
ここで、
$$z=[x, y, \dot{x}, \dot{y}]^\top$$
とおくと、運動方程式は以下のようになります。
$$\dot{z} = \left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \frac{1}{m}F_x \\ \frac{1}{m}F_y \end{array} \right] $$
また、入力値に$-1 \leq F_x \leq 1, -1 \leq F_y \leq 1 $という制約を付けます。
最適制御のPythonコード
最適制御問題をCasADiを使って解く、Pythonコードを示します。
物体のパラメータと微分方程式モデル
まず、物体のパラメータと微分方程式モデルを設定します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
import numpy as np
import pandas as pd
import casadi as ca
import matplotlib.pyplot as plt
Ts = 1.0 # サンプリング周期[s]
N = 20 # サンプリング点数
m = 1 # 質量[kg]
# 運動方程式を微分方程式で記述する
z = ca.MX.sym('z', 4) # x, y, x_dot, y_dot
u = ca.MX.sym("u", 2)
zdot = ca.vertcat(z[2], z[3], u[0]/m, u[1]/m)
# 初期・終端状態
z0 = [0, 0, 0, 0]
zf = [20, 15, 0, 0]
# Objective term
L = (z[0]-zf[0])**2 + (z[1]-zf[1])**2 + u[0]**2 + u[1]**2
dae = {'x': z,
'p': u,
'ode': zdot,
'quad':L}
opts = {'tf':Ts}
F = ca.integrator('F', 'cvodes', dae, opts)
|
サンプリング周期を1[s], サンプリング点数をN=20とするので、シミュレーション全体の時間は20秒です。また、物体の質量mは適当な値としています。
初期位置を (x, y)=(0, 0), 終端位置を (x, y)=(20, 15)とし、いずれの速度も0とします。
Lは毎ステップ計算する評価関数です。毎ステップのLを足し合わせるため、最適化問題の評価関数は以下になります。
$$\mathrm{minimize} \sum_{k=0}^{N} (x[k]-20)^2 + (y[k]-15)^2 + F_x[k]^2 + F_y[k]^2$$
すなわち、物体がなるべく早く目標位置に近づくようにして、かつ入力の値も小さくします。
optsのtfには、微分方程式を実行する時間を指定しています。
最適化問題の定式化
次に、最適化問題を定式化します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
w = []; lbw = []; ubw = []; G = []; J = 0
# 変数とその上下限、等式制約、評価関数
Xk = ca.MX.sym('X', 4)
w += [Xk]
lbw += z0
ubw += z0
for i in range(N):
Uk = ca.MX.sym(f'U{i}', 2)
w += [Uk]
lbw += [-1, -1]
ubw += [1, 1]
Fk = F(x0=Xk, p=Uk) # Tsだけシミュレーションする（微分方程式を解く）
J += Fk["qf"]
Xk = ca.MX.sym(f'X{i+1}', 4)
w += [Xk]
G += [Fk['xf'] - Xk]
if i != N-1:
lbw += [-100, -100, -100, -100]
ubw += [100, 100, 100, 100]
else:
# 最終ステップでは、位置誤差±1, 速度誤差±1以下
lbw += zf
ubw += zf
prob = {'f': J, 'x': ca.vertcat(*w), 'g': ca.vertcat(*G)}
option = {"ipopt.print_level": 4}
solver = ca.nlpsol('solver', 'ipopt', prob, option)
sol = solver(x0=0, lbx=lbw, ubx=ubw, lbg=0, ubg=0)
|
wは最適化問題の未知変数ベクトルで、毎ステップの物体の位置・速度・入力になります。
その次のfor文の内側で、サンプリング周期Tsだけ物体の移動に関する微分方程式を解くことをN回だけ繰り返します。
G += [Fk['xf'] - Xk]では、「ある時間幅の最終状態と次の時間幅の初期状態の差」を制約としてリストに追加しています。後述のlbg=0, ubg=0によってGの全要素が0, すなわち次の時間幅と状態が連続するようにしています。
また、最適化問題を解くために非線形ソルバIPOPTを使用しています。
ここまでのコードを実行すると、以下のログが表示され、最適化問題を解けたことが分かります。実行時間は549ミリ秒でした。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
Total number of variables............................: 116
variables with only lower bounds: 0
variables with lower and upper bounds: 116
variables with only upper bounds: 0
Total number of equality constraints.................: 80
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
Number of Iterations....: 20
(scaled) (unscaled)
Objective...............: 2.0550680493859359e+003 2.0550680493859359e+003
Dual infeasibility......: 4.7876970893711765e-009 4.7876970893711765e-009
Constraint violation....: 7.4005512828989595e-010 7.4005512828989595e-010
Complementarity.........: 3.1755690494319810e-009 3.1755690494319810e-009
Overall NLP error.......: 4.7876970893711765e-009 4.7876970893711765e-009
Number of objective function evaluations = 21
Number of objective gradient evaluations = 21
Number of equality constraint evaluations = 21
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 21
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 20
Total CPU secs in IPOPT (w/o function evaluations) = 0.022
Total CPU secs in NLP function evaluations = 0.526
EXIT: Optimal Solution Found.
solver : t_proc (avg) t_wall (avg) n_eval
nlp_f | 17.00ms (809.52us) 16.94ms (806.48us) 21
nlp_g | 19.00ms (904.76us) 18.95ms (902.52us) 21
nlp_grad_f | 87.00ms ( 3.95ms) 86.79ms ( 3.94ms) 22
nlp_hess_l | 337.00ms ( 16.85ms) 338.04ms ( 16.90ms) 20
nlp_jac_g | 72.00ms ( 3.27ms) 71.84ms ( 3.27ms) 22
total | 549.00ms (549.00ms) 549.63ms (549.63ms) 1
|
また、最適化結果をPandasのDataFrameに格納してみます。
1
2
3
4
|
x_star = np.array(sol["x"].elements() + [np.nan]*2)
x_star = x_star.reshape(-1, 6)
x_star = pd.DataFrame(x_star, columns=["x","y","x_dot","y_dot","Fx","Fy"])
print(x_star)
|
実行結果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
x y x_dot y_dot Fx Fy
0 0.000000 0.000000 0.000000 0.000000 1.000000 1.000000
1 0.500000 0.500000 1.000000 1.000000 1.000000 1.000000
2 2.000001 2.000001 2.000000 2.000000 1.000000 1.000000
3 4.500006 4.500006 3.000000 3.000000 1.000000 0.979165
4 8.000017 7.989599 4.000000 3.979165 0.239390 -1.000000
5 12.119718 11.468738 4.239390 2.979165 -1.000000 -1.000000
6 15.859081 13.947875 3.239390 1.979165 -1.000000 -1.000000
7 18.598438 15.427006 2.239390 0.979165 -1.000000 -1.000000
8 20.337789 15.906131 1.239390 -0.020835 -1.000000 -0.431016
9 21.077138 15.669770 0.239390 -0.451851 -0.776128 0.117231
10 20.928398 15.276545 -0.536737 -0.334620 0.073027 0.196229
11 20.428192 15.040086 -0.463710 -0.138391 0.249498 0.118196
12 20.089285 14.960818 -0.214212 -0.020195 0.169356 0.039711
13 19.959810 14.960492 -0.044857 0.019516 0.064839 0.000239
14 19.947434 14.980128 0.019982 0.019755 0.006297 -0.009784
15 19.970590 14.994952 0.026280 0.009972 -0.011596 -0.007437
16 19.991027 15.001176 0.014683 0.002534 -0.010442 -0.003163
17 20.000451 15.002118 0.004241 -0.000628 -0.005049 -0.000519
18 20.002129 15.001226 -0.000807 -0.001147 -0.000925 0.000467
19 20.000832 15.000327 -0.001732 -0.000680 0.001732 0.000680
20 20.000000 15.000000 0.000000 0.000000 NaN NaN
|
おおよそ10秒程度で、目標位置 (x, y)=(20, 15)に到達しています。
最適化結果のプロット
最後に最適化結果をプロットします。まず、x-y座標上の物体の動きを示します。
1
2
3
4
5
6
|
fig, ax = plt.subplots()
ax.plot(x_star["x"], x_star["y"])
ax.grid()
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.show()
|
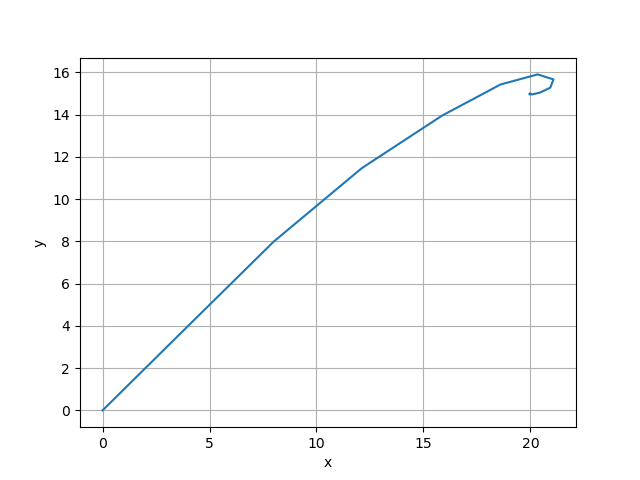
初期位置 (x, y)=(0, 0)から目標位置の (x, y)=(20, 15)に移動しています。目標位置をややオーバーシュートしています。
次に、制御入力をプロットします。
1
2
3
4
5
6
7
8
9
|
fig, ax = plt.subplots(nrows=2, sharex=True)
ax[0].plot(x_star.index, x_star["Fx"])
ax[1].plot(x_star.index, x_star["Fy"])
for i in range(2):
ax[i].grid()
ax[0].set_ylabel("Fx")
ax[1].set_ylabel("Fy")
ax[1].set_xlabel("Time")
plt.show()
|
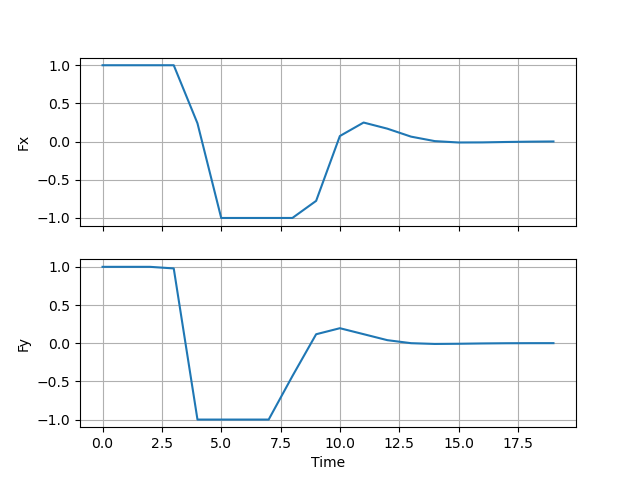
制御入力は制約（±1）の範囲であることが分かります。
まとめ
Pythonと最適化ライブラリCasADiを使って、Direct Multiple Shooting法と呼ばれる手法によって最適制御問題を解きました。
参考
CasADiの公式リファレンス
