はじめに
複数の要素から構成される最適化モデルを最適化ライブラリPyomoで実装するとき、コードを再利用しやすくするため、各要素をクラスとして実装する方法を検討しました。
複数の要素から構成されるモデルとは以下のようなものです。
- ビルの空調システム（個々の部屋や空調装置が要素）
- 発送電システム（個々の発電装置や受電装置、蓄電装置が要素）
要素をクラスとして実装することにより、異なる構成のシステムにコードを再利用しやすくなります。
検討に使用したPythonとPyomoのバージョンは以下の通りです。
| ソフトウェア |
バージョン |
| Python |
3.9.7 |
| Pyomo |
6.4.1 |
CasADi+Python版の記事は以下です。
数理最適化モデルの要素をクラスとして実装するプラクティス【CasADi+Python編】 – Helve Tech Blog
例題とするシステム
例題とするシステムは、画像のように4つのプロセス（要素）から構成されています。各プロセスを通過する量$x_1, …, x_4$が大きいほど利益が多くなるとします。また、$x_1, …, x_4$にはそれぞれ上限があるとします。
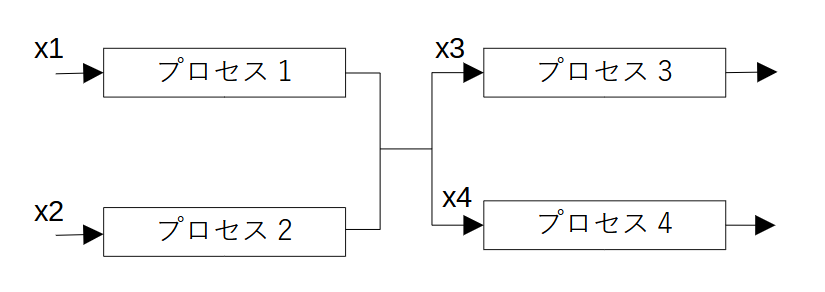
最適化問題を次式のように定義します。システムを通過する量の和は6とします（最後の制約式）。
$$ \max \ x_1 + 2x_2 + 3x_3 + x_4 \\ \mathrm{s.t.} \ x_1 \le 5 \\ x_2 \le 3 \\ x_3 \le 3 \\ x_4 \le 5 \\ x_1 + x_2 = x_3 + x_4 \\ x_1 + x_2 = 6 $$
要素をクラス化した実装例
プロセスをProcessクラスとして実装した最適化のコードを以下に示します。__init__メソッドで変数や制約式を定義します。
proc1.xやproc2.profitのように、最適化の変数をインスタンス変数として扱うことができます。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
import pyomo.environ as pe
class Process:
count = 0
def __init__(self, mdl, x_ub, unit_profit):
# オブジェクト名、変数、パラメータ、制約式を設定する
name = "proc"+str(Process.count)
self.name = name
Process.count += 1
exec(f"mdl.{name}_x = pe.Var(domain=pyo.Reals, bounds=(0, x_ub))")
exec(f"self.x = mdl.{name}_x")
exec(f"mdl.{name}_unit_profit = pe.Param(default=unit_profit)")
exec(f"self.unit_profit = mdl.{name}_unit_profit")
exec(f"mdl.{name}_profit = pe.Expression(expr = mdl.{name}_unit_profit*mdl.{name}_x)")
exec(f"self.profit = mdl.{name}_profit")
mdl = pe.ConcreteModel()
proc1 = Process(mdl, 5, 1)
proc2 = Process(mdl, 3, 2)
proc3 = Process(mdl, 3, 3)
proc4 = Process(mdl, 5, 1)
mdl.const1 = pe.Constraint(expr = proc1.x + proc2.x == proc3.x + proc4.x)
mdl.const2 = pe.Constraint(expr = proc1.x + proc2.x == 6)
mdl.obj = pe.Objective(expr=proc1.profit + proc2.profit + proc3.profit + proc4.profit,
sense = pe.maximize)
opt = pe.SolverFactory('glpk')
res = opt.solve(mdl, tee=False)
print(f"Objective: {mdl.obj()}")
for v in mdl.component_data_objects(ctype=pe.Var):
print(f"{v.name=}, {v.lb=}, {v.value=}, {v.ub=}")
|
実行結果
実行すると、以下のように最適化結果が表示されます。
1
2
3
4
5
|
Objective: 21.0
v.name='proc1_x', v.lb=0, v.value=3.0, v.ub=5
v.name='proc2_x', v.lb=0, v.value=3.0, v.ub=3
v.name='proc3_x', v.lb=0, v.value=3.0, v.ub=3
v.name='proc4_x', v.lb=0, v.value=3.0, v.ub=5
|
例題では4つのプロセスの構造（制約式やパラメータ）が同じであるため、クラスを1つしか作りませんが、異なる構造のプロセスがある場合、その分だけ対応したクラスを作成します。
要素クラスの解説
要素のProcessクラスを解説します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Process:
count = 0
def __init__(self, mdl, x_ub, unit_profit):
# 変数、パラメータ、制約式を設定する
name = "proc"+str(Process.count)
self.name = name
Process.count += 1
exec(f"mdl.{name}_x = pe.Var(domain=pe.Reals, bounds=(0, x_ub))")
exec(f"self.x = mdl.{name}_x")
exec(f"mdl.{name}_unit_profit = pe.Param(default=unit_profit)")
exec(f"self.unit_profit = mdl.{name}_unit_profit")
exec(f"mdl.{name}_profit = pe.Expression(expr = mdl.{name}_unit_profit*mdl.{name}_x)")
exec(f"self.profit = mdl.{name}_profit")
|
変数self.nameはオブジェクトの名前（プロセスの固有の名前）です。self.nameはオブジェクト固有の変数名を付けるために使用します。
Pyomoでは、最適化の変数やパラメータ、制約式をModelオブジェクト（コードでは変数mdl）の変数として定義します。すなわち、同じクラスで複数の要素（プロセス）を定義する場合、変数名が重複しないようにします。そのため、exec関数を使っています。
Varクラスで最適化の変数を定義しています。Realsは実数であることを設定し、boundsは変数の上限・下限で指定します。
Paramでパラメータ（最適化計算中も一定値の変数）を定義します。default引数に値を渡します。
Expressionクラスで式を定義します。ここでは、{name}_profit = mdl.{name}_unit_profit*mdl.{name}_xという関係式を定義しています。
また、mdlの変数をオブジェクト変数にも格納しています。これは、評価関数などを定義するときに、オブジェクトの外側から変数にアクセスしやすくするためです。
クラス化しない場合のコード
クラス化しない場合のコード例を示します。変数をベクトル化した場合、もう少し簡潔に記述できます。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
mdl = pe.ConcreteModel()
mdl.proc1_x = pe.Var(domain=pe.Reals, bounds=(0, 5))
mdl.proc1_unit_profit = pe.Param(default=1)
mdl.proc1_profit = pe.Expression(expr = mdl.proc1_unit_profit*mdl.proc1_x)
mdl.proc2_x = pe.Var(domain=pe.Reals, bounds=(0, 3))
mdl.proc2_unit_profit = pe.Param(default=2)
mdl.proc2_profit = pe.Expression(expr = mdl.proc2_unit_profit*mdl.proc2_x)
mdl.proc3_x = pe.Var(domain=pe.Reals, bounds=(0, 3))
mdl.proc3_unit_profit = pe.Param(default=3)
mdl.proc3_profit = pe.Expression(expr = mdl.proc3_unit_profit*mdl.proc3_x)
mdl.proc4_x = pe.Var(domain=pe.Reals, bounds=(0, 5))
mdl.proc4_unit_profit = pe.Param(default=1)
mdl.proc4_profit = pe.Expression(expr = mdl.proc4_unit_profit*mdl.proc4_x)
mdl.const1 = pe.Constraint(expr = mdl.proc1_x + mdl.proc2_x\
== mdl.proc3_x + mdl.proc4_x)
mdl.const2 = pe.Constraint(expr = mdl.proc1_x + mdl.proc2_x == 6)
mdl.obj = pe.Objective(expr=mdl.proc1_profit+mdl.proc2_profit+mdl.proc3_profit+mdl.proc4_profit,
sense = pe.maximize)
opt = pe.SolverFactory('glpk')
res = opt.solve(mdl, tee=False)
print(f"Objective: {mdl.obj()}")
for v in mdl.component_data_objects(ctype=pe.Var):
print(f"{v.name=}, {v.lb=}, {v.value=}, {v.ub=}")
|
