はじめに #
Scikit-learnの回帰木やランダムフォレスト回帰のクラスには、Feature Importances (FI) という説明変数の重要度を示す指標があるが、導出について公式のリファレンスに書かれていなかったため調べた。 結論から述べると、各説明変数による予測誤差の二乗平均の減少量に対して、データ点数の重みを掛けて求めた値である。
記事執筆時点でのバージョンは以下の通り。
| ソフトウェア | バージョン |
|---|---|
| Python | 3.6.5 |
| Scikit-learn | 0.19.1 |
回帰木のFI #
ランダムフォレスト回帰は、複数の回帰木の集合であるので、初めに回帰木のFIを確認する。
公式リファンレスには、FIについて以下のように記述されている。
The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance. sklearn.tree.DecisionTreeRegressor — scikit-learn 0.24.0 documentation
すなわち、説明変数ごとに、ジニ重要度 (Gini importance) と呼ばれる基準量の減少量を(正規化したものを)合算して得られる、とある。 しかし、ネット上にはGini importanceに関する目ぼしい資料は見つからなかった(ジニ係数やジニ特徴量に関する資料はあるが)。
そこで、自分でプログラムを動かして動作を確認する。
まず、3つの説明変数X0, X1, X2と、目的変数Yを用意し、
DecisionTreeRegressorで学習させる。
import numpy as np
import pandas as pd
from sklearn import tree
X0 = np.array([0,0,1,1]).reshape(-1, 1)
X1 = np.array([0,1,0,0]).reshape(-1, 1)
X2 = np.array([0,0,0,1]).reshape(-1, 1)
X = np.hstack([X0, X1, X2])
Y = np.array([1,2,3,4])
t = tree.DecisionTreeRegressor(max_depth=3, random_state=0)
t.fit(X, Y)
回帰木をGraphVizで可視化する。
tree.export_graphviz(t, "tree.dot")
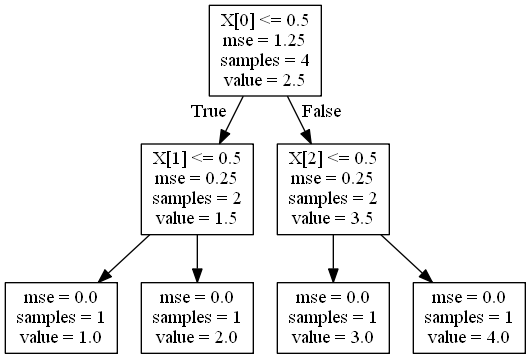
図の四角は、回帰木の各ノードを示す。 四角の中の説明は以下の通り。
- 1行目の不等式が成り立つ場合は、左側のノードに進む。成り立たない場合は、右のノードに進む。
- mse は平均二乗誤差 (MSE, Mean Squared Error) 。
- samples はデータ点数。
- value は予測値。
この中で、mseとsamplesに着目する。
1段目のノードでは、X0 (X[0])によって、4点のデータのMSEが1.25から0.25に減少している。
また、2段目のノードでは、X1 (X[1]), X2 (X[2])によって、それぞれ分岐後の2点のデータのMSEが0.25から0に減少している。
次にFIを表示する。
print(pd.Series(t.feature_importances_, index=["X0", "X1", "X2"]))
実行結果
X0 0.8
X1 0.1
X2 0.1
ここで、X0, X1, X2によるMSEの減少量に対してデータ点数を掛けると、それぞれ、
X0: (1.25 - 0.25)*4 = 4
X1: (0.25 - 0)*2 = 0.5
X2: (0.25 - 0)*2 = 0.5
となる。
減少量の合計が1となるように正規化すると、
X0: 4/(4+0.5+0.5) = 0.8
X1: 0.5/(4+0.5+0.5) = 0.1
X2: 0.5/(4+0.5+0.5) = 0.1
となり、FIと一致している。
すなわち、FIは予測誤差の二乗平均の減少量に対して、データ点数の重みを掛けて正規化した値となる。
ランダムフォレスト回帰のFI #
ランダムフォレストのFIの計算方法についても、Scikit-learnの公式リファレンスには書かれていない。
しかし、ソースコードを見ると、決定木ごとにFIが計算され、それらの平均がランダムフォレストのFIとなっている(scikit-learnのforest.py 359~375行目、BaseForestクラスより。このクラスは、RandomForestRegressorが継承している)。
@property
def feature_importances_(self):
"""Return the feature importances (the higher, the more important the
feature).
Returns
-------
feature_importances_ : array, shape = [n_features]
"""
check_is_fitted(self, 'estimators_')
all_importances = Parallel(n_jobs=self.n_jobs,
backend="threading")(
delayed(getattr)(tree, 'feature_importances_')
for tree in self.estimators_)
return sum(all_importances) / len(self.estimators_)
