Scikit-learnでデータをスケール変換する

はじめに

Pythonの機械学習用ライブラリScikit-learnに実装されている、スケール変換について調べた。スケール変換を行うクラス3つのパラメータとメソッドをまとめ、各変換の結果を比較した。

スケール変換は、扱う数値データを何らかの規則で変換するものである。機械学習で桁数の異なるデータをまとめて扱うときには、スケール変換がほぼ必須となる。
通常、ニューラルネットワークやSVM（サポートベクターマシン）では、スケール変換をしないとなかなか学習が進まない。ただし、ランダムフォレスト等の決定木を使う手法ではスケール変換は不要である。

この記事では、以下3つのスケール変換方法を扱う。

StandardScaler: 標準化（平均0, 分散1）
RobustScaler: 外れ値に頑健な標準化
MinMaxScaler: 正規化（最大1, 最小0）

2021/01/28 標準偏差と分散を誤って記述している箇所があったため修正。

環境

記事執筆時点で使用したライブラリのバージョンは以下の通り。

ソフトウェア	バージョン
Python	3.6.5
Scikit-learn	0.19.1
NumPy	1.14.3
matplotlib	2.2.2

Pythonで以下の通りライブラリをインポートする。Scikit-learnのpreprocessingモジュールにスケール変換処理がまとめられている。

1
2
3


import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing

以下、各スケール変換のパラメータとメソッドについてまとめた結果を記す。

標準化（平均0, 分散1）する

データの平均値と分散を変換する操作を標準化と呼ぶ。平均値を0, 分散を1とすることが多い。変換操作は以下の式で表される。
$$ Y = \frac{X-\mu}{\sigma} $$
ここで、$Y$は変換後のデータ、$X$は変換前のデータである。また、$\mu, \sigma$は、それぞれ$X$の平均、標準偏差である（$\sigma^2$は分散）。

Scikit-learnで標準化は、
関数としてはscale,
クラスとしてはStandardScaler
という名前で用意されている。

StandardScalerクラスを使うと、あるデータに対して行った変換を別のデータに対して適用できる。
機械学習の場合、学習データに対して行った変換を、検証データに対して行うので、実用上はStandardScalerを使う機会が多いと思う。そのため、本記事ではStandardScalerのみ扱う。

StandardScalerのパラメータ

1

preprocessing.StandardScaler(copy=True, with_mean=True, with_std=True)

StandardScalerクラスの主なパラメータの説明は以下の通り。基本的に全てデフォルトのまま使う。

copy
ブール型。デフォルト値はTrue.
Falseの場合、transformやfit_transformメソッドで変換時に、変換元のデータを破壊的に変換する。Trueの場合、元のデータは変換されない。

with_mean
ブール型。デフォルト値はTrue.
Trueの場合、平均値を0とする。
Falseの場合、以下の変換になる。
$Y = \frac{X}{\sigma}$
分散は1になるが、平均が維持されるとは限らない。

with_std
ブール型。デフォルト値はTrue.
Trueの場合、分散を0とする。
Falseの場合、以下の変換になる。
$Y = X-\mu$
分散は変化せず、平均は0となる。

StandardScalerのメソッド

良く使うメソッドは次の3つ。
fit(X)
配列Xの平均と標準偏差を計算して、記憶する（変換は行わない）。

transform(X)
配列Xに変換を施して、変換後の配列を返す。

fit_transform(X)
配列Xに対して、fitとtransformを同時に行う。

なお、2次元配列を変換する場合、縦 (axis=0) 方向に変換が行われる。

StandardScalerの使用例

以下の2次元配列xを用意する。

1
2
3
4


x = np.arange(0, 8, 1.).reshape(-1, 2)
print(x)
print(x.mean(axis=0))
print(x.std(axis=0))

実行結果

1
2
3
4
5
6


[[0. 1.]
 [2. 3.]
 [4. 5.]
 [6. 7.]]
[3. 4.]
[2.23606798 2.23606798]

第0列目の平均は3, 標準偏差は2.24,
第1列目の平均は4, 標準偏差は2.24である。

次に、xを標準化する。

1
2
3
4
5
6
7
8


sscaler = preprocessing.StandardScaler() # インスタンスの作成

sscaler.fit(x)           # xの平均と標準偏差を計算
y = sscaler.transform(x) # xを変換

print(y)
print(y.mean(axis=0))
print(y.std(axis=0))

実行結果
以下の通り、変換後の配列yは各列とも平均は0, 標準偏差は1となった。

1
2
3
4
5
6


[[-1.34164079 -1.34164079]
 [-0.4472136  -0.4472136 ]
 [ 0.4472136   0.4472136 ]
 [ 1.34164079  1.34164079]]
[0. 0.]
[1. 1.]

ここで、

1
2


sscaler.fit(x)           # xの平均と標準偏差を計算
y = sscaler.transform(x) # xを変換

は、以下と同じである。

1

y = sscaler.fit_transform(x) # xを変換した結果が返る

外れ値に頑健な標準化

変換前のデータに極端に大きな値または小さな値が含まれていた場合、標準化を行うと大きく結果が変わってしまう。これを避けるため、データの四分位点を基準にして標準化を行う方法がある。

Scikit-learnでこのような変換は、
関数としてはrobust_scale,
クラスとしてはRobustScaler
という名前で用意されている。
本記事ではRobustScalerのみ扱う。

RobustScalerの変換操作は以下の式で表される。
$$ Y = \frac{X-Q_2}{Q_3-Q_1} $$
ここで、$Y$は変換後のデータ、$X$は変換前のデータである。
また、$Q_1, Q_2, Q_3$は、それぞれ$X$の第1～第3四分位点である。
標準化と比較すると、元のデータの平均が$Q_2$（中央値）、標準偏差が$Q_3-Q_1$であると仮定しているとも考えられる。
なお、上の式の分母で、どの範囲（パーセンタイル）のデータを使うかは設定で変更可能である。

RobustScalerのパラメータ

1
2


preprocessing.RobustScaler(with_centering=True, with_scaling=True, 
                           quantile_range=(25.0, 75.0), copy=True)

RobustScalerクラスの主なパラメータの説明は以下の通り。
外れ値の多さに対して、quantile_rangeを変更する。

with_centering
ブール型。デフォルト値はTrue.
Trueの場合、データから中央値を引いて、平均を0とする。

with_std
ブール型。デフォルト値はTrue.
Trueの場合、quantile_rangeで選択したパーセンタイルのデータの差でデータを割る。

quantile_range
タプル型。デフォルト値は(25.0, 75.0).
標準化を行うデータの範囲をパーセンテージで指定する。
(25.0, 75.0)の場合、下位25%と上位25%にある値の差でデータ全体を割る。
また、特徴量が複数ある場合、それぞれの特徴量に対して数値が選ばれる。
なお、データの値は、NumPyのpercentile関数で取得している。
この関数は、パーセンタイルとデータ数が一致しない場合、補間して返す。そのため、データ数が少ない場合や、離散的な場合は注意する。

copy
ブール型。デフォルト値はTrue.
Falseの場合、transformやfit_transformメソッドで変換時に、変換元のデータを破壊的に変換する。
Trueの場合、元のデータは変換されない。

RobustScalerのメソッド

StandardScalerと同じく、良く使うメソッドは次の3つ。
fit(X)
transform(X)
fit_transform(X)

RobustScalerの使用例

以下の2次元配列xを用意する。

1
2
3
4


x = np.arange(0, 8, 1.).reshape(-1, 2)
print(x)
print(x.mean(axis=0))
print(x.std(axis=0))

実行結果

1
2
3
4
5
6


[[0. 1.]
 [2. 3.]
 [4. 5.]
 [6. 7.]]
[3. 4.]
[2.23606798 2.23606798]

第0列目の平均は3, 標準偏差は2.24,
第1列目の平均は4, 標準偏差は2.24である。

次に、xを標準化する。下位25%と上位25%、すなわち[0. 1.]と[6. 7.]が無視される。

1
2
3
4
5
6
7
8


rscaler = preprocessing.RobustScaler(quantile_range=(25., 75.))

rscaler.fit(x)
y = rscaler.transform(x[1:3])

print(y)
print(y.mean(axis=0))
print(y.std(axis=0))

実行結果
以下の通り、変換後の配列yは各列とも平均は0, 標準偏差は0.745となった。

1
2
3
4
5
6


[[-1.         -1.        ]
 [-0.33333333 -0.33333333]
 [ 0.33333333  0.33333333]
 [ 1.          1.        ]]
[0. 0.]
[0.74535599 0.74535599]

正規化（最大1, 最小0）する

データの最大値と最小値を制限する変換を正規化と呼ぶ。最大値を1, 最小値を0とすることが多い。
変換操作は以下の式で表される。
$$Y = \frac{X-x_{\min}}{x_{\max}-x_{\min}}$$

ここで、$Y$は変換後のデータ、$X$は変換前のデータである。
また、$x_{\min}, x_{\max}$は、それぞれ$X$の最小値、最大値である。

Scikit-learnで正規化は、
関数としてはminmax_scale,
クラスとしてはMinMaxScaler
という名前で用意されている。

標準化と同様に、本記事ではMinMaxScalerクラスのみ扱う。

MinMaxScalerのパラメータ

1

preprocessing.MinMaxScaler(feature_range=(0, 1), copy=True)

MinMaxScalerクラスの主なパラメータの説明は以下の通り。
feature_range
タプル型。デフォルト値は(0, 1).
変換後の最大値、最小値を設定する。

copy
ブール型。デフォルト値はTrue.
Falseの場合、transformやfit_transformメソッドで変換時に、
変換元のデータを破壊的に変換する。
Trueの場合、元のデータは変換されない。

MinMaxScalerのメソッド

StandardScalerと同じく、良く使うメソッドは次の3つ。
fit(X)
transform(X)
fit_transform(X)

MinMaxScalerの使用例

標準化と同じ2次元配列xを用意する。

1
2
3
4


x = np.arange(0, 6, 1.).reshape(-1, 2)
print(x)
print(x.min(axis=0))
print(x.max(axis=0))

実行結果

1
2
3
4
5


[[0. 1.]
 [2. 3.]
 [4. 5.]]
[0. 1.]
[4. 5.]

第0列目の最小値は0, 最大値は4,
第1列目の最小値は1, 最大値は5である。

次に、xを正規化する。

1
2
3
4
5
6
7
8


mmscaler = preprocessing.MinMaxScaler() # インスタンスの作成

mmscaler.fit(x)           # xの最大・最小を計算
y = mmscaler.transform(x) # xを変換

print(y)
print(y.min(axis=0))
print(y.max(axis=0))

実行結果
以下の通り、変換後の配列yは各列とも最小値は0, 最大値は1となった。

1
2
3
4
5


[[0.  0. ]
 [0.5 0.5]
 [1.  1. ]]
[0. 0.]
[1. 1.]

ここで、

1
2


mmscaler.fit(x)           # xの平均と分散を計算
y = mmscaler.transform(x) # xを変換

としたのは、以下のようにしても同じ結果となる。

1

y = mmscaler.fit_transform(x) # xを変換した結果が返る

各変換の比較

2次元のデータを対象として、スケール変換の効果を散布図で確認する。
各変換のパラメータはデフォルトとした。

ケース1：平均(0, 0), 分散1

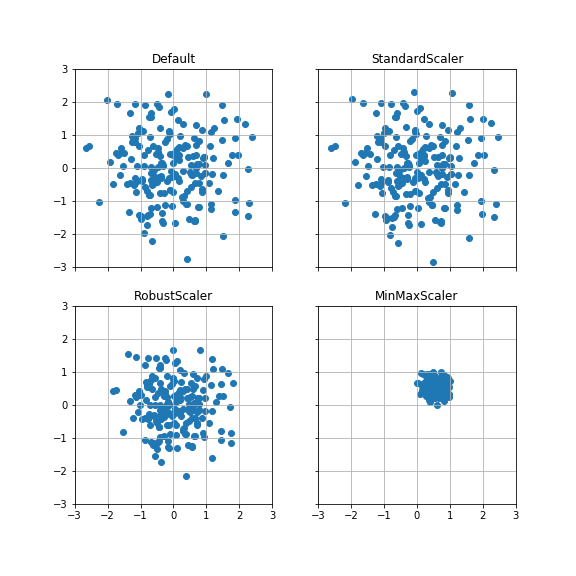
平均が原点、分散が各方向に1の正規分布データ200点を変換する。
StandardScalerは、変換前とほとんど変わらない。
RobustScalerは、StandardScalerよりも分散が小さくなっている。
また、MinMaxScalerは縦方向・横方向ともに0～1の範囲に収まっている。
sklearn-case1

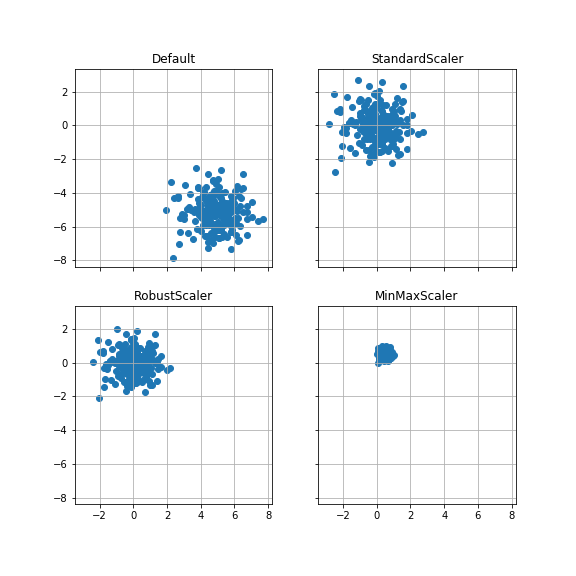
ケース2：平均(5, -5), 分散1

平均が(5, -5), 分散が各方向に1の正規分布データ200点を変換する。
StandardScalerは、データの分布形状をほぼ保ったまま変換できている。
sklearn-case2

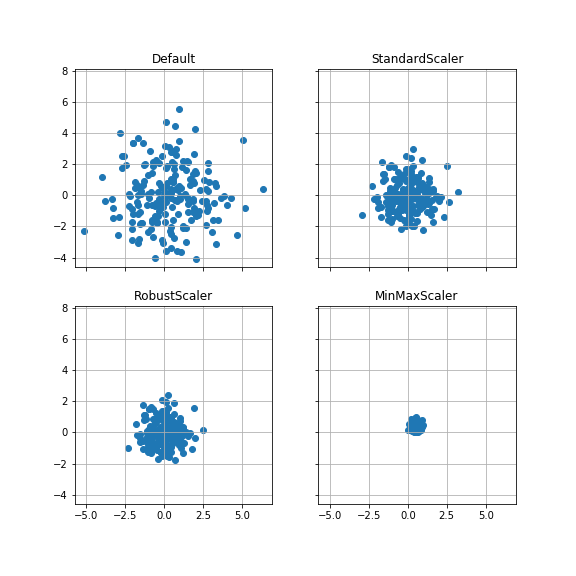
ケース3：平均(0, 0), 分散4

平均が(0, 0), 分散が各方向に4とした正規分布データ200点を変換する。
分散が4（標準偏差が2）なので、各方向とも-2～2の範囲に約68.27%, -4～4の範囲に約95.45%のデータがある。
StandardScalerでは分散が約半分となり、-1～1の範囲に約68.27%, -2～2の範囲に約95.45%のデータがあることになる。
sklearn-case3

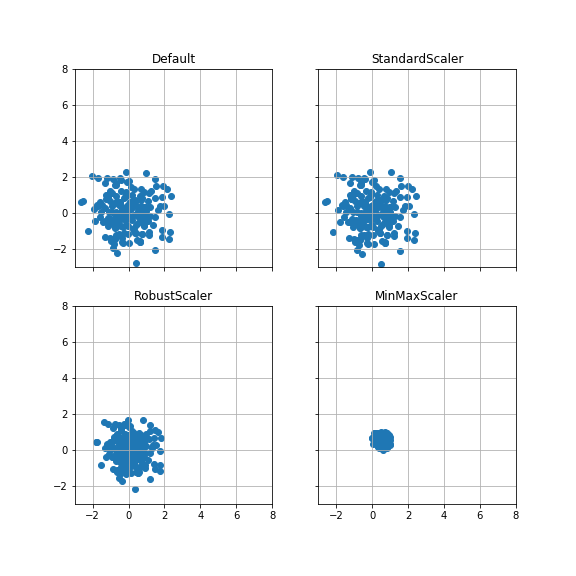
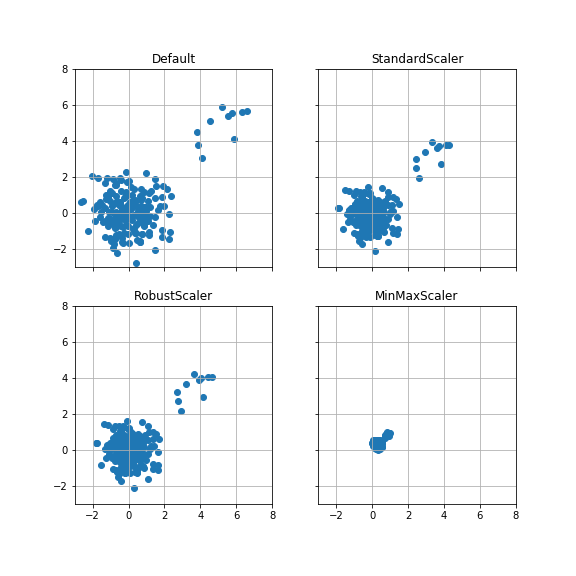
ケース4：外れ値を加えた場合

ケース1のデータに、平均(5, 5), 分散1のデータを10点追加する。
ケース1の散布図をスケールを揃えて比較する。
RobustScalerでは、外れ値を除く分布の形状が、外れ値を加える前と後で変化していない。
一方、StandardScaler, MinMaxScalerでは、分布の形状が外れ値によって変化している。
ケース1（外れ値なし）
sklearn-case1a
ケース4（外れ値あり）
sklearn-case4

ケース1～4のソースコードは以下の通り。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


def plotScaler(x, xlim=(None, None), ylim=(None, None)):
    sscaler = preprocessing.StandardScaler()
    rscaler = preprocessing.RobustScaler()
    mmscaler = preprocessing.MinMaxScaler()
    
    xs = sscaler.fit_transform(x)
    xr = rscaler.fit_transform(x)
    xm = mmscaler.fit_transform(x)
    
    fig, ax = plt.subplots(nrows=2, ncols=2, sharex=True, sharey=True, figsize=(8,8))
    ax[0,0].scatter(x[:,0], x[:,1])
    ax[0,0].set_title("Default")
    ax[0,1].scatter(xs[:,0], xs[:,1])
    ax[0,1].set_title("StandardScaler")
    ax[1,0].scatter(xr[:,0], xr[:,1])
    ax[1,0].set_title("RobustScaler")
    ax[1,1].scatter(xm[:,0], xm[:,1])
    ax[1,1].set_title("MinMaxScaler")
    for i in range(ax.shape[0]):
        for j in range(ax.shape[1]):
            ax[i,j].axis("square")
            ax[i,j].grid()
    ax[1,1].set_xlim(xlim)
    ax[1,1].set_ylim(ylim)
    plt.show()

np.random.seed(0)

# ケース1: 平均(0,0),  分散１
x1 = np.random.randn(200, 2)
plotScaler(x1, xlim=(-3, 3), ylim=(-3, 3))

# ケース2: 平均(5,-5), 分散１
x2_0 = np.random.randn(200, 1)+5
x2_1 = np.random.randn(200, 1)-5
x2   = np.hstack([x2_0, x2_1])
plotScaler(x2)

# ケース3: 平均(0,0), 分散4
x3 = np.random.randn(200, 2)*2
plotScaler(x3)

# ケース4: ケース1に(5, 5), 分散１の外れ値を10点追加
x4_0 = np.random.randn(10, 2)+5
x4 = np.vstack([x1, x4_0]) 
plotScaler(x1, xlim=(-3, 8), ylim=(-3, 8))
plotScaler(x4, xlim=(-3, 8), ylim=(-3, 8))