はじめに #
複数の要素から構成される最適化モデルを最適化ライブラリCasADiとPythonで実装するとき、コードを再利用しやすくするため、各要素をクラスとして実装する方法を検討しました。
複数の要素から構成されるモデルとは以下のようなものです。
- ビルの空調システム(個々の部屋や空調装置が要素)
- 発送電システム(個々の発電装置や受電装置、蓄電装置が要素)
要素をクラスとして実装することにより、異なる構成のシステムにコードを再利用しやすくなります。
検討に使用したPythonとCasADiのバージョンは以下の通りです。
- Python 3.9.7
- CasADi 3.5.5
例題とするシステム #
例題とするシステムは、画像のように4つのプロセス(要素)から構成されています。各プロセスを通過する量\(x_1, ..., x_4\)が大きいほど利益が多くなるとします。また、\(x_1, ..., x_4\)にはそれぞれ上限があるとします。
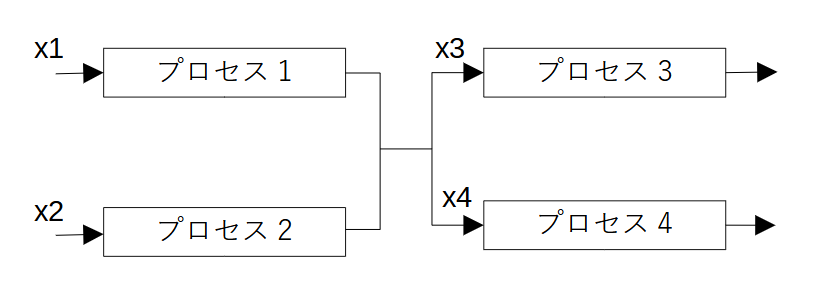
最適化問題を次式のように定義します。システムを通過する量の和は6とします(最後の制約式)。
$$ \max \ x_1 + 2x_2 + 3x_3 + x_4 \\\ \mathrm{s.t.} \ x_1 \le 5 \\\ x_2 \le 3 \\\ x_3 \le 3 \\\ x_4 \le 5 \\\ x_1 + x_2 = x_3 + x_4 \\\ x_1 + x_2 = 6 $$要素をクラス化した実装例 #
プロセスをProcessクラスとして実装した最適化のコードを以下に示します。__init__メソッドでは、変数や制約式を定義します。get_variablesメソッドは、最適化計算の後、変数の値を取得するためのメソッドです。
proc1.xやproc2.profitのように、最適化の変数をインスタンス変数として扱うことができます。
import casadi as ca
class Process:
def __init__(self, name, opti, x_ub, unit_profit):
# 変数とパラメータ、制約式を設定する
self.name = name
self.x = opti.variable()
opti.subject_to(opti.bounded(0, self.x, x_ub))
self.unit_profit = opti.parameter()
opti.set_value(self.unit_profit, unit_profit)
self.profit = self.unit_profit*self.x
def get_variables(self):
# 変数を辞書で返す
return {f"{self.name}_x": self.x}
opti = ca.Opti()
variables = {}
proc1 = Process("proc1", opti, 5, 1)
variables.update(proc1.get_variables())
proc2 = Process("proc2", opti, 3, 2)
variables.update(proc2.get_variables())
proc3 = Process("proc3", opti, 3, 3)
variables.update(proc3.get_variables())
proc4 = Process("proc4", opti, 5, 1)
variables.update(proc4.get_variables())
opti.subject_to(proc1.x + proc2.x == proc3.x + proc4.x)
opti.subject_to(proc1.x + proc2.x == 6)
obj = proc1.profit + proc2.profit + proc3.profit + proc4.profit
opti.minimize(-obj)
opti.solver('ipopt')
sol = opti.solve()
print(f"Objective: {sol.value(obj)}")
for key, var in variables.items():
print(f"{key}: {sol.value(var)}")
実行結果 #
実行すると、以下のように最適化結果が表示されます。
Objective: 21.00000008498571
proc1_x: 2.9999999725075446
proc2_x: 3.0000000274924554
proc3_x: 3.0000000287466273
proc4_x: 2.999999971253373
例題では4つのプロセスの構造(制約式やパラメータ)が同じであるため、クラスを1つしか作りませんが、異なる構造のプロセスがある場合、その分だけ対応したクラスを作成します。
要素クラスの解説 #
要素のProcessクラスを解説します。
class Process:
def __init__(self, name, opti, x_ub, unit_profit):
# 変数とパラメータ、制約式を設定する
self.name = name
self.x = opti.variable()
opti.subject_to(opti.bounded(0, self.x, x_ub))
self.unit_profit = opti.parameter()
opti.set_value(self.unit_profit, unit_profit)
self.profit = self.unit_profit*self.x
def get_variables(self):
# 変数を辞書で返す
return {f"{self.name}_x": self.x}
引数nameにはオブジェクトの名前(プロセスの固有の名前)を渡します。この引数は最適化には直接関係せず、固有の変数名を名付けるためのものです(get_variablesメソッドを参照)。
opti.variable()で最適化の変数xを定義します。また、opti.subject_toで変数に対する制約式を定義します。
opti.parameter()でパラメータ(最適化計算中も一定値の変数)を定義します。パラメータの値はopti.set_value()メソッドで設定します。
さらに、self.profit = self.unit_profit*self.xのように、ある変数(ここではunit_profitとx)から別の変数を定義することも可能です。
get_variablesは、変数名と変数を辞書で戻すメソッドとなっています。このメソッドは実状に応じて、必要な情報(変数の上限・下限など)を返すように改良できます。
クラス化しない場合のコード #
クラス化しない場合のコード例を示します。変数をベクトル化した場合、もう少し簡潔に記述できます。
opti = ca.Opti()
variables = []
proc1_x = opti.variable()
opti.subject_to(opti.bounded(0, proc1_x, 5))
proc1_unit_profit = opti.parameter()
opti.set_value(proc1_unit_profit, 1)
proc1_profit = proc1_unit_profit*proc1_x
proc2_x = opti.variable()
opti.subject_to(opti.bounded(0, proc2_x, 3))
proc2_unit_profit = opti.parameter()
opti.set_value(proc2_unit_profit, 2)
proc2_profit = proc2_unit_profit*proc2_x
proc3_x = opti.variable()
opti.subject_to(opti.bounded(0, proc3_x, 3))
proc3_unit_profit = opti.parameter()
opti.set_value(proc3_unit_profit, 3)
proc3_profit = proc3_unit_profit*proc3_x
proc4_x = opti.variable()
opti.subject_to(opti.bounded(0, proc4_x, 5))
proc4_unit_profit = opti.parameter()
opti.set_value(proc4_unit_profit, 1)
proc4_profit = proc4_unit_profit*proc4_x
opti.subject_to(proc1_x + proc2_x == proc3_x + proc4_x)
opti.subject_to(proc1_x + proc2_x == 6)
obj = proc1_profit + proc2_profit + proc3_profit + proc4_profit
opti.minimize(-obj)
opti.solver('ipopt')
sol = opti.solve()
print(f"Objective: {sol.value(obj)}")
print(f"proc1_x: {sol.value(proc1_x)}")
print(f"proc2_x: {sol.value(proc2_x)}")
print(f"proc3_x: {sol.value(proc3_x)}")
print(f"proc4_x: {sol.value(proc4_x)}")
